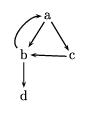
Figure 7.3: A sample graph.



arcs( a, [b,c] ). arcs( b, [a,d] ). arcs( c, [b] ). arcs( d, [] ).
Naively, we might define a path/3 predicate for this graph in essentially the same way that we implemented it for trees, that is, by simply taking the reflexive transitive closure of the arc relation, compactly encoded by the arcs/2 predicate.

Figure 7.3: A sample graph.
path( X, Y, [] ) :- X = Y.
path( X, Y, P ) :-
arcs( X, ArcList ),
member( Z, ArcList ),
P = [Z|PTail],
path( Z, Y, PTail ).
This technique, where we simulate breadth-first search using repeated bounded depth-first searches actually has a name: it is called iterative deepening. Here each successive call to path/3, in effect, deepens the search by one level of the search tree.list([]). list([_|L]):- list(L). ?- list(P), path(a,Y,P ).
path( X, Y, P ) :- % path/3 redefined
path( X, Y, [X], P ).
path( X, X, Path, Path ).
path( X, Y, PIn, POut ) :-
arcs( X, L ),
member( Z, L ),
nonmember( Z, PIn ), % Been here before?
path( Z, Y, [Z|PIn], POut ).
?- path( a, d, P ).then this code will begin by initializing the ``path-so-far'' argument to a list containing only the starting point of the search. Then we call path/4, which does the real work. When we finally reach our destination, and the base clause applies, then we simply pass the contents of the ``path-so-far'' argument PIn over to the output argument POut. This is then passed up to the calling goal and from it to the goal that called it, and so on up the chain of recursive calls to path/4 and thence to path(a,d,P), our original goal. Note that whereas in path/3 we actually built up the path ``on the way up out'' of the recursion, here we are building it up ``on the way down in.'' This means that at every point, we can see where we have been so far, by examining the PIn variable. In this case we do that with a call to nonmember/2.
neq( Node1, Node2 ) :-
neq_arcs( Node1, L ),
member( Node2, L ).
neq_arcs( a, [b,c,d] ).
neq_arcs( b, [a,c,d] ).
neq_arcs( c, [a,b,d] ).
neq_arcs( d, [a,b,c] ).
graph( 1, [a/[b,c],
b/[a,d],
c/[b],
d/[]
] ).
Accordingly, we reimplement path so that it includes an argument position for the graph itself.?- graph( G ), path( a, d, G, P ).
path( From, To, Graph, [From|Path] ) :-
p( From, To, Graph, Path ).
p( X, Y, _G, [] ) :- X = Y.
p( X, Y, G, [Z|P] ) :-
select( X/Arcs, G, SmallerG ),
member( Z, Arcs ),
p( Z, Y, SmallerG, P ).
dft/4, if the call to
select/3 fails, we must simply ignore that node and
continue. Therefore we need a call to nonmember_/2 so as to
be certain that we only ignore nodes that we really have already
visited. Similarly, where p/4 calls member/2 to
nondeterministically select one way to extend its current path,
dft/4 must execute a recursion on the entire list of
neighbors, so as to check all ways to traverse the graph.
df_traversal(GIn,[Root|Route]):-
GIn = [Root/Neighbors|GInRest], % get the root's neighbors
dft(Neighbors,GInRest,_GOut,Route).
dft([],RemainingG,RemainingG,[]).
dft([N|RestNs],GIn,GOut,[N|Route]):-
select(N/Nbrs,GIn,SmallerG),
dft(Nbrs,SmallerG,EvenSmallerG,RfromN),
dft(RestNs,EvenSmallerG,GOut,RfromRest),
append(RfromN,RfromRest,Route).
dft([N|RestNs],GIn,GOut,Route):-
nonmember_(N,GIn), % already visited
dft(RestNs,GIn,GOut,Route).
The predicate nonmember_/2 which is called in clause 3 of
df_search_2/3 is not quite the same as the predicate
nonmember/2 we have seen before, although it is about as much different
from that predicate as its name implies. The trick is that we are
asking whether or not a node is still present in a graph
and a graph is not a list of nodes, but a list of node/adjacency-list
pairs. The code for nonmember_/2 looks like the following and
assumes that neq/2 has been implemented.
nonmember_( _, [] ).
nonmember_( X, [Y/_|L] ) :-
neq( X, Y ),
nonmember_( X, L ).


