7.1 Practically everything is a graph
The last data structures we will consider before moving on to more
process-oriented topics are graphs. Graphs are, formally,
collections of objects, called nodes, together with a binary
relation which connect pairs of nodes, and which can be visualized
diagrammatically as a collection of line segments or arrows between
pairs of nodes. The relation is called the edge relation of the graph
(or the arc relation, if it is asymmetric). Thinking in terms of
diagrams, we call the arrows arcs and the line segments
edges. Graphs can be either directed (in which case we
use arcs to connect the nodes) or undirected (in which case we
use edges: we think of an edge as standing for a pair of arcs going
there and back again). We have already seen several examples of
directed graphs: trees are a special case of directed graph, and also
the transition diagrams for finite state automata and Turing machines
are directed graphs.
Both the nodes and the edges of graphs can bear labels. Finite state
automata, for example, bear labels on their arcs. Syntax trees (e.g.,
phrase structure trees in linguistics, or graphical representations of
expression trees in general) are examples of graphs with labels on
their nodes. There exist also many graphs in which both nodes and arcs
are labeled. One important example of this is typed feature
structures which play a large role in computational linguistics
and, increasingly, in logic programming in general. Examples of
undirected graphs are rarer in computational linguistics, although
they are very common in artificial intelligence research. A road map
which indicates distance in kilometers between points is an example of
an undirected graph: the distance is the same no matter which
direction you travel. There are many applications of this essential
idea, of weighted graphs, in knowledge representation, and
these are important in computational linguistics in representing the
lexicon, especially. Another important class of undirected graphs are
constraint graphs, which are used to help solve many hard
combinatorial problems, where the choice of a value for one variable
has consequences for the possible values of other variables. Then
nodes can be used to represent the variables, and edges are labeled
with constraints that relate these variables.
Formally, graphs are very simple. They are just binary relations over
an arbitrary set. Note that this set, the set of nodes, can really
contain anything at all. As long as we do not need to worry too much
about the internal details of our nodes, they can be pretty much
anything. Given such a set---let us call it N, for ``nodes''---we
consider next the set of all pairs of nodes, that is, the cartesian
product N× N. A binary relation R on N is just a subset of
N× N:
R Í N× N
If this set of pairs, this relation, is symmetric, that is, if
for every pair (x,y) which we find in R we can also find its
inverse (y,x) , then the graph áN,Rñ is
undirected.
We can add more structure to this basic notion easily. For example, we
could add a set of node labels---let us call it S---and
a function l: N ® S which assigns labels to
nodes. Similarly, we could define a (partial) two-place function
mapping pairs of nodes (i.e., edges or arcs) to some predefined set of
arc labels (which might be disjoint from S). Alternatively, we
can extend the arc-relation to a 3-place relation like
arc(Node1,Label,Node2). This has the advantage that it actually
``looks like'' an arc in a, well, graphical representation of a
graph.
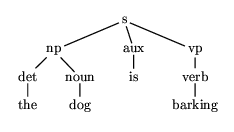
Consider, for example, the expression
s(np(det(the),noun(dog)),aux(is),vp(v(barking)))
This corresponds to the expression tree which we can draw as in
figure 7.1
Figure 7.1: A phrase structure tree is a graph too.
This tree in turn corresponds to a graph of the following sort.
The choice of node names is arbitrary. We can, for example,
use tree-addresses to name the nodes of the graph.
N = {e, 1, 2, 3, 11, 111, 12, 121, 2, 21, 3, 31, 311 }
Then our graph has the following edges.
|
R |
= { |
(e,1), (e,2), (e,3),
(1,11), (1,12), (11,111), (12,121), |
| |
|
(2,21), (3,31), (31,311) } |
Furthermore, given a set of labels like
S = {the, dog, is, barking, s, np, det, noun,
aux, vp, verb }
then we can define a node-labeling function as follows.
| l :
e |
|® s |
| 1 |
|® np |
| 11 |
|® det |
| 111 |
|® the |
| 12 |
|® noun |
| 121 |
|® dog |
| |
·
·
·
|
Note that this function is itself a graph! Its nodes are drawn from
both N and S of the previous expression-tree graph, and its
arcs are defined by the |® relation. It is, to be sure, a
rather special sort of graph: every node has at most one arc leading
out of it, for example. (This is what makes a relation a function,
after all.) But it is a legitimate graph nonetheless and many
general-purpose graph processing algorithms actually make perfect
sense when applied to the graph of a function.
Trees too are rather special instances of graphs. First, they are
rooted. That is, there is a single node from which all other
nodes can be reached by travelling along the arcs from node to
node. Furthermore, though any given node can have any number of arcs
leading away from it, no node ever has more than one arc leading into
it. (The root has none, every other node has one.) Equivalently: there
is exactly one path from the root to every node of the tree. Finally,
in all of the examples we have considered, the nodes of the tree were
interpreted as being in some definite left-to-right order. This is in
fact not always assumed, even for trees: what we have been looking at
are often called, specifically, ordered trees. Still less is
this a condition on graphs in general. Finally, a tree contains no
cycles. That is, though every node is an ancestor of itself, no node
is a proper ancestor of itself. If you travel down the tree you
will never find yourself above where you started! So trees are rooted,
ordered, directed, acyclic graphs having for every node a unique path
from the root.
7.1.1 Representing Graphs
In Prolog, all data structures are encoded as logical terms,
and logical terms, being expression trees, are a fortiori
trees (ordered trees, in particular). Graphs, in their full
generality, disobey many of the conditions that define trees. There
can be many ``roots'', that is, there can be any number of nodes from
which all other nodes are accessible. There may be nodes which are not
accessible from any other node. Since a node can have
arbitrarily many incoming as well as outgoing arcs, it is no longer
true that every node has a unique parent. One result of this is that
it very often makes no sense to think of nodes as being left-to-right
ordered. Finally, we need to allow for loops: now we have structures
with a finite number of nodes and a finite number of edges, but having
also infinitely long paths!
So the very first problem we face is that
we can no longer encode the data of interest directly as Prolog
terms. We will have to define terms (i.e., expression trees)
which bear a more abstract relation to the actual data objects.
What this means in practical terms is that we can no longer count on
the data structure definition to give us the skeleton of an
all-purpose graph-processing algorithm. In writing solutions to
problems over graphs we have to concentrate more on the intended
semantics of our data structures and less on their raw syntactic
structure.
Let us try to get clearer what we mean by ``abstractness'' here,
because it will have definite computational consequences. When we
design data structures we have in mind beforehand some particular kind
of mathematical structure which we want to represent. Individual data
structures then denote individual structures of the relevant
sort. Up until now this denotation relation has been pretty direct and
concrete. Let us look at some examples.
We write [[T]] for the denotation of a Prolog expression
tree T. Then we can assign denotations to successor terms
in terms of the structure of ordinary arithmetic
with the following rules.
|
[[0]] |
= |
0 |
| [[s(N)]] |
= |
1 + [[N]]
|
Observe first that every natural number has a unique successor term
representation. Also, the clauses in the definition of the denotation
function exactly mirror the clauses in the data type definition.
In a similar way we can assign denotations to lists in terms of
strings. A full definition is complicated by the fact that we can
have lists of lists; we restrict ourselves here to the case of lists
whose members are all drawn from a particular alphabet, given
in advance. Then, writing uw for the concatenation of
string u with string w, we have the following rules.
|
[[[]]] |
= |
e (the empty sequence) |
| [[[H|T]]] |
= |
H[[T]]
|
Finally, we can assign denotations to tree data structures in terms
of trees. Again, we restrict ourselves to the case where the node
labels of our trees range only over a set of symbols given in advance.
|
[[R/[]]] |
= |
R |
| [[R/[T1,...,Tn]]] |
= |
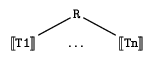
|
With both lists and trees there is a unique data structure for each
individual in the target structures, and the clauses defining the
denotation function mirror closely the clauses defining the data type.
Finally, we think of lists and trees as ways of storing
information. In this connection we note that there is a difference
between a position in a list, for example, and the term which is
stored there, and the same thing holds for trees. In particular, a
single data item can be stored in many different positions in a list
or a tree. But ``the third position in list L,'' defines a
unique individual: two things which are both the third position in
list L must necessarily be the same thing. Similarly with
trees: there may be many different occurrences of the label
np in a tree, but there is at most one node which is the
second daughter of the first dauther of the second daughter of the
root. In what follows we will refer to as labels the data items
we are storing in a structure, that is, the things which can appear
any number of times. We will refer to as names the descriptions
we use to pick out individual storage locations. We observe
immediately that there is a one-to-one relation between storage
locations in a list or tree data type and individuals (string
positions or tree nodes) in their intended denotations.
These are all properties which we will not be able to maintain when we
try to represent (general) graphs.
The simplest representation (though not the most efficient) is to
encode the set of graph nodes as a list of node names and the
arc relation as a list of pairs of node names. For example,
the arc relation for the tree in figure 7.1
could be represented (rather sloppily) as the list
[arc(s,np), arc(np,det), arc(det,the), arc(np,noun), arc(noun,dog),
... ]
Note that this encoding of the graph collapses the arc relation and
the node labeling function. We can only use this trick when each node
has a unique label! If for example we constructed the phrase structure
tree for the sentence the dog is barking at a cat, which
contains a second noun phrase---a cat---then we might have
two nodes both mapped to the symbol np.
Then we would risk
confusing the paths leading out of the first np-node with those
leading out of the second!
The difference between a node name and a node label is
a little subtle but it boils down to just exactly this point. Many
nodes can share the same label, but if two nodes have the same
name then they are the same node.
In this case we would need something like the
less-readable approach illustrated below,
where R encodes the arc relation of the graph and
L encodes the labeling function (as another graph).
R = [arc(e,1), arc(1,11), arc(11,111), arc(1,12), arc(12,121),...],
L = [arc(e,s), arc(1,np), arc(11,det), arc(111,the), arc(12,noun),
arc(121,dog),...]
Of course, these two graphs do not have to be kept distinct.
LR = [arc(arc(e,s),arc(1,np)), arc(arc(1,np),arc(11,det)),... ]
We can make this easier to read! We could use an infix function symbol
for the labeling arcs,
LR2 = [arc(e-s,1-np), arc(1-np,11-det),...]
or, perhaps even better, we could reverse the order of the arguments,
treating the node names as ``subscripts'' on the category labels.
LR3 = [arc(s-e,np-1), arc(np-1,det-11),...]
We can, of course, also use an infix function symbol for the dominance
arcs. Let's say, oh, to pick one at random, suppose we use `/'?
LR4 = [(s-e)/(np-1), (np-1)/(det-11), (np-1)/(noun-12),...]
Now things are maybe starting to look more familiar. We can take one
more step in this direction, in fact, if we associate with each node a
list of its outgoing arcs:
LR5 = [(s-e)/[np-1,aux-2,vp-3], (np-1)/[det-11,noun-12],
(det-11)/[the-111], (the-111)/[],...]
This is pretty much as close as we can get to our representation of trees as
`/'-terms, and still allow ourselves a representation which is
flexible enough to encode general graphs.1
This kind of representation gives a Prolog version of a common approach
to representing graphs using adjacency lists. We have a
list of structures which pair each node with a list of its immediate
``neighbors'' in the graph. This representation is abstract in the
sense that there can be several occurrences of a given node-name in
this structure: once on the left of the `/' symbol and maybe many
times in the adjacency lists of other nodes. Yet each occurrence of
this node-name expression is meant to denote exactly the same node in
the graph which the data structure ``means''.
So there are many nodes in the adjacency list expression tree which
correspond to a particular individual node in the intended graph.
We have thus the following correspondence.
|
|
|
|
| names |
| labels |
¬¾ |
names |
| |
|
labels
|
Therefore our
graph-processing predicates must adhere to this intended
interpretation which is not given ``for free'' in the data structure.
This means that the essential processing step in a graph-predicate
will be one in which a node-name found in some adjacency list is used
as a key to access that node's own adjacency structure from the list.
More concretely, suppose we want to get from node a to node
c via node b. First, the symbol b must appear in a's
adjacency list.
Graph = [...,a/[...,b,...],...]
Then the node named b must have its own record in the graph
structure:
Graph = [...,b/BsNeighbors,...]
Presumably c is one of b's neighbors, that is,
BsNeighbors = [...,c,...].
Finally, c has its own record in the graph Graph. Once we
access that record, we can say that our procedure has moved from
a to c in the graph. The key step, semantically, is the one
in which we behave as if the occurrence of b, say, in a's
adjacency list was directly connected to the occurrence of b in
the expression that b/BsNeighbors is meant to match. Compare this
with the situation in tree structures. The ``occurrence'' of a node as
one node's daughter and the ``occurrence'' of that node as the root of
its subtree are in fact the same occurrence of that symbol. In the
case of graphs we actually have to do some extra processing (namely by
searching the graph for an occurrence of b/BsNeighbors) to
enforce this semantic identity of two distinct (but, okay, very
similar looking) syntactic objects.
There are some minor variations on this theme which are sometimes
useful. First, we can easily accomodate arc labels in this
representation. We simply code entries in the adjacency list as
(arc-label, node) pairs, and nodes, as before, as (node-name, node-label)
pairs. So, for example, we might have
[(1-s)/[subj-(2-np),pred-(3-vp)],...]
In some circumstances we may be able to use the position of a node's
adjacency record in the graph as the name of that node. Suppose that
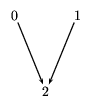
we have the unlabeled graph in figure 7.2.
Figure 7.2: A sample graph with no labels.
We can represent this simply as the following list of lists.
[[2],[2],[]]
We can use calls to a suitable version of nth/3 to access
nodes. (By ``suitable'' we mean that in this case it must treat the
first element of a list as element number 0.)
Note before we go on that there is one other way of representing
graphs which may have occurred to you already if you thought about the
finite state automaton example. Since the arc-relation is, after all,
a relation, and since Prolog programs are, after all, ways of defining
relations, we can represent graphs directly as Prolog programs.
arcs( s-e, [np-1,aux-2,vp-3] ).
arcs( np-1, [det-11, noun-12] ).
arcs( det-11, [the-111] ).
arcs( the-111, [] ).
...
This obviously won't work if we are using a graph which we intend to
modify, or create from scratch.2
But it works well when we are given a graph which represents some
static data structure which we want to use, but not to modify. The
finite state automaton's delta-relation is a good example of
this. Similarly, a graph representing distances between cities is also
a good example of such static data. For most natural language
applications, a semantic network encoding the lexicon may be expected
never to change while a program is running, though here, with the
possibility of sophisticated learning algorithms and so forth, the
case is not quite so clear cut.