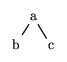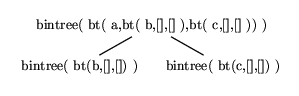Chapter 6 Trees

6.1 Trees: Lists with Bushy Tails

If all of our data structures (and even our programs!) are ultimately expression trees, then we should expect to spend a lot of time manipulating trees. Indeed, inasmuch as natural numbers in successor notation and lists are expression trees, we have already spent some time doing just that. But lists and natural numbers are rather special cases of trees. These structures are of course technically trees, but they're really not very `tree-like'. What does this mean? What does it mean to be ``essentially tree-like?'' Let's begin by comparing the technical recursive/inductive definitions of successor-notation and lists, and see how we can make the concepts we find there more general.

Definition of NN:
1. Basic = {0 },
2. Gen = {F_s }, where we define F_s as follows:
  F_s( t ) = s(t).
Definition of Lists:
1. Basic = {[] },
2. Gen = {F_exp | exp is an expression tree }, where we define F_exp as follows:
  
  F
  
  exp
  ( t ) = [exp|t] .

We observed in the last section that these structures are similar in that their generator functions take only a single argument. To obtain trees, we simply relax this restriction and allow generator functions which take multiple arguments. So with successor notation and lists we have trees with an essentially linear structure, because the functions which generate them are recursive in only one argument position. Trees, whose generator functions are polyadic, not necessarily monadic, are multiply recursive and essentially nonlinear because their generator functions are recursive in several argument places. So we have essentially the following hierarchy of generalizations:

The natural numbers form a mathematical structure with a single monadic function.
The lists form a mathematical structure with many monadic functions.
The trees form a mathematical structure with many polyadic functions.

For our purposes it is perhaps best to think of a tree as being like a `sequence' with one head and multiple tails, each of which is (recursively) itself a `sequence' with one head and multiple tails, each of which is ...

  list( L ) :- empty( L ).
  list( L ) :- 
      head( L, _ ),
      tail( L, LTail ),
      list( LTail ).   

  tree( T ) :- leaf( T ).
  tree( T ) :- 
      root( T, _ ),            % ``head''
      subtrees( T, SubTrees ), % ``tails''
      forest( SubTrees ).      % Is each tail a tree?  

  forest( LT ):- empty_forest( LT ).
  forest( LT ) :- 
      first( LT, LT_First ), 
      rest( LT, LT_Rest ), 
      tree( LT_First ), 
      forest( LT_Rest ).

Essentially, we treat the root of a tree as we would treat the head of a list: this is the main similarity between trees and lists. On the other hand, the multiply recursive nature of trees means that a whole new dimension is introduced into our treatment of a tree's tails. That is, the definition of the tree data type given here is doubly recursive. Intuitively, we must travel recursively down the tree and also across the sequence of subtrees at any given node.

6.1.1 How to write trees

In the case of lists, there was a special representation already built into Prolog. In the case of trees we are on our own. So the way of encoding trees which I will present to you here should in no way be considered the absolute and inviolable standard way to do things. There is much more variety among programs and programmers in representations for trees than there is in representations of sequences. We will use the following scheme to encode trees.

First, we define a forest to be a list of trees. So we can define empty_forest/1 as the empty list, [], and first/2 and rest/2 as the head and tail of a list, respectively. So the definition of forest/1 can be rewritten as follows.

  forest( [] ).
  forest( [T1|RestTs] ) :- 
      tree( T1 ), 
      forest( RestTs ).

A tree is the pairing of a root with a (possibly empty) forest of subtrees. So we need some 2-place functor to tie these two data items together. Here we will use `/'/2, the division symbol. Because this can be written infixed between its arguments, it makes tree terms a little more readable. Once again: there is nothing sacred in this representation; in particular, one might prefer a prefixed functor like t or even tree. Using the scheme we have adopted here, though, we would implement tree/1 as follows.

  tree( _Root/[] ).\quad\% A leaf has no subtrees.
  tree( _Root/SubTrees ) :-
      SubTrees = [_|_],\quad\% SubTrees is non-empty;
      forest( SubTrees ).

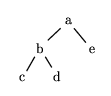
For example, we would represent the tree

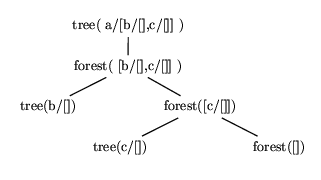
as the Prolog term a/[ b/[], c/[] ]. The proof that this is a tree is straightforward and is summarized in figure 6.1.

Figure 6.1: Proof tree for the goal: ?- tree(a/[b/[],c/[]]).

The definition I have given in tree/1 is very general. Often we can take advantage of particular circumstances to derive more restricted definitions. One of the most common subtypes of tree is the binary tree. A binary tree is a tree in which every node has exactly two or zero subtrees. We have already seen one example of this structure: lists are a sort of binary tree, except that they are only recursive in their second subtree. We can represent binary trees as 3-place functions, with one argument for the root, as usual, and the other two argument places for the left subtree and the right subtree.

  bintree( bt( Root, [], [] ) ).
  bintree( bt( Root, LTree, RTree ) ) :- 
      bintree( LTree ), 
      bintree( RTree ).

Clearly we can generlize this to trinary, quaternary and in general n-ary trees, for any fixed n, as follows.

  ntree( n( Root, [], ... , [] ) ).
  ntree( n( Root, T1, ... , Tn ) ) :- 
      ntree( T1 ), 
      ... , 
      ntree( Tn ).

Our original example was a binary tree. Recoding it as a bintree would yield the following term.

bt( a, bt( b, [], [] ), bt( c, [], [] ) )

The representation of the data structure is less readable, perhaps (though no `one-dimensional' representation of a tree will ever be really readable!), but we can process binary trees without ever calling anything like forest/1. That is, instead of one call to tree/1 and one to forest/1, we have two calls to bintree/1. The proof tree corresponding to figure 6.1 is given in figure 6.2. Note that the proof tree in this case much more closely reflects the structure of the underlying tree. With our more flexible slash-notation we have to focus on the calls to tree/1 and ignore the calls to forest/1, treating them as essentially just some sort of glue.

Figure 6.2: Proof tree for the goal ?- bintree( bt( a,bt( b,[],[] ),bt( c,[],[] )) ).

6.2 Climbing Around in a Tree

From time to time we will need to process a tree in a way which requires that we visit every node in the tree exactly once. This would be the case if, for example, the tree represented an arithmetic expression which we wished to evaluate, or a boolean expression which we wished to test for satisfiability. The simplest such application is the case where we just want to list the labels of all the nodes in a tree, or print them out. We will begin with binary trees, and then return to the general case.

There are essentially three ways to traverse a binary tree, each yielding a sequence of nodes with exactly the same members, but in a different order. These three traversal orders, preorder inorder and postorder, are described informally in figure 6.3.

preorder --- process the root,

then the left subtree,

then the right subtree;

inorder --- process the left subtree,

then the root,

then the right subtree;

postorder --- process the left subtree,

then the right subtree,

then the root.

Figure 6.3: The three basic traversal orders, for binary trees.

Consider then the three implementations of printtree/2 given in figure 6.4. The first will print the list of nodes in preorder, the second in inorder and the third in postorder. (The Prolog builtin predicate write/1 prints out a term on the computer screen. The term ' ' is just a space typed between quotes; it is a legal constant, since anything between quotes is a legal constant.) Note that everything is identical in all three versions except the order of the subgoals in the recursive clauses.

      printtree_1( bt(Label,[],[]) ).
      printtree_1( bt(Label,Left,Right) ) :- 
          printlabel( Label ), 
          printtree_1( Left ), 
          printtree_1( Right ).
      
      printtree_2( bt(Label,[],[]) ).
      printtree_2( bt(Label,Left,Right) ) :- 
          printtree_2( Left ),
          printlabel( Label ),
          printtree_2( Right ).
      
      printtree_3( bt(Label,[],[]) ).
      printtree_3( bt(Label,Left,Right) ) :- 
          printtree_3( Left ), 
          printtree_3( Right ), 
          printlabel( Label ).
      
      printlabel( X ) :- write( X ), write( ' ' ).

Figure 6.4: Printing a tree, in preorder, inorder and postorder.

With general trees the situation is only slightly more complex. In place of two calls to printtree we need to call a second predicate print_trees which will print out sequences of trees of any length. Then the code for the recursive clause of printtree_1 becomes

  printtree_1( Label/Subtrees ) :- 
      printlabel( Label ),
      print_trees_1( Subtrees ).

Then the definition for a postorder traversal just reverses the order of the goals in the body of printtree_1. The definition of an inorder traversal is more complicated. In the first place, given a tree with, say, four subtrees, we have the option of processing the first subtree, then the label, then the rest, or else the first then the second then the label then the rest, and so on. So for example we might use a clause like

  printtree_2( Label/[LeftCorner|Rest] ) :-
      printtree_2( LeftCorner ),
      printlabel( Label ),
      print_trees_2( Rest ).

The definitions of the various print_trees_i differ only which version of printtree they call.

6.2.1 Pretty-printing Trees

A slightly more sophisticated---and extremely useful---example is the following. It ``pretty-prints'' a tree, that is, prints it in a format which reflects not only the content of the tree, but also its structure. With printtree/1 all we got was the content.

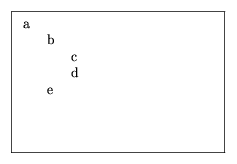
Pretty_print/1 prints out a tree as follows. We define a tab stop to be four spaces. Then each label will be printed as many tab stops from the left margin as it has ancestors in the tree. That is, the root node will be printed at the left margin (0 ancestors, 0 tab stops), its immediate subtrees will be printed 1 tab stop from the margin, and so on. For example, the tree a/[b/[c/[],d/[]],e/[]], i.e.,

will be printed as in figure 6.5.

Figure 6.5: Pretty-printer output.

We begin by defining a ``shell predicate'' pretty_print/1, which simply initializes the tab stop to zero and calls the main predicate pp_tree/2. The code is given in figure 6.6; it follows closely the data structure definition tree/1, as we would expect.

      pretty_print( Tree ) :-
          Tab = 0, 
          pp_tree( Tab, Tree ).
      
      pp_tree( Tab, Label/[] ) :- \%\ Print a leaf.
          print_label( Tab, Label ).
      pp_tree( Tab, Label/SubTrees ) :- 
          SubTrees = [_|_], 
          print_label( Tab, Label ), 
          NewTab is Tab + 4, 
          pp_subtrees( NewTab, SubTrees ).
      
      pp_subtrees( _, [] ).
      pp_subtrees( Tab, [Next|Rest] ) :- 
          pp_tree( Tab, Next ), 
          pp_subtrees( Tab, Rest ).
      
      print_label( Tab, Label ) :- 
          tab( Tab ), 
          write( Label ), 
          nl.

Figure 6.6: Simple pretty printer for trees.

Several new predicates are introduced in this example which are built in to Prolog, which is why we did not present their definitions in figure 6.6. First the predicate is/2, which is defined as an infix operator, and so is written between its two arguments, does arithmetic evaluation. It uses the computer's own native arithmetic abilities, and so is much more efficient than the code we defined in Chapter 4. However, this efficiency is only gained with some sacrifice. The ``predicate'' is/2 is not truly relational: it requires absolutely that its first argument be a variable or a numeral and its second argument be a term which (a) represents an arithmetic expression and (b) contains no uninstantiated variables. Note that the first argument can be an instantiated variable, in which case a call to is/2 simply checks that the number instantiating its first argument is indeed the value of the expression in its second argument. However, if any variable term in the second argument has not been instantiated (to a number or other fully instantiated arithmetic expression), then Prolog will halt and report an error. The predicate is/2 is thus non-logical in its behavior, and therefore should be used with care or the logical interpretation of your program will disappear.

The remaining builtin predicates used in defining pretty_print/1 handle the output of information directly to the terminal screen while the program is running. Logically, they have the same meaning as true/0, a constant which always succeeds. Procedurally, however, they have side effects, namely they cause the user's terminal to display the given information. The builtin tab/1 simply prints the number of spaces specified in its single argument. The builtin write/1 writes out the term given in its argument. Note that ' ' (a space enclosed in single quotes) is a perfectly legitimate term, as is ', ' (a comma followed by a space, all enclosed in single quotes): anything enclosed in single quotes counts as a constant term. So we can do a fair amount of formatting this way, though it is not necessary here. Finally, the builtin nl/0 simply prints a carriage return (``nl'' stands for ``new line'').

Pretty_print/1 is an example of a preorder traversal of a tree.

6.3 Generalizations of some predicates on lists

A number of the things we can do with lists we will want to do also with trees. For example, we had member/2, which would search lists for us.

                member( X, [X|_] ).
                member( X, [_|L] ) :- 
                        member( X, L ).

The analogous predicate for trees we will call tmember/2. It is defined so that tmember( X, Tree ) is true just in case X is the label on a node in Tree. There are actually two senses in which something can be a ``member'' of a tree: it can be a node in the tree, or it can be a subtree of the tree. It is the former we are most interested in here, but in fact the two problems are closely related, and we begin by defining subtree/2.

                subtree( Tree, Tree ).
                subtree( LittleT, BigT ) :- 
                        BigT = _/SubTrees, 
                        member( MiddleT, SubTrees ), 
                        subtree( LittleT, MiddleT ).

Since our representations of trees are in part constructed out of lists, it should be no surprise to see member/2 appear in our predicates for searching trees. Here now is the code for tmember/2.

                tmember( X, X/_ ).
                tmember( X, BigT ) :- 
                        BigT = _/SubTrees, 
                        member( MiddleT, SubTrees ), 
                        tmember( X, MiddleT ).

As promised, it is extremely similar in form to subtree/2. After all, nodes are just the roots of subtrees and subtrees are just the set of nodes dominated by their roots.

I have argued that trees are rather like lists in two dimensions. We have seen that we can use our standard list predicates to good effect by applying them to the lists of subtrees at any particular node. We can mimic this ``horizontal'' use of list processing in the ``vertical'' dimension in a fairly direct manner once we provide ourselves with a definition of a path in a tree. The following predicate, which defines paths, can be used either to determine if a given list of expressions labels a branch from the root to the frontier of a tree or else to generate/enumerate the paths in a given tree.

                path( [X], X/[] ). 
                path( [X|Xs], X/STs ) :- 
                        member( ST, STs ), 
                        path( Xs, ST ).

So, for example, we could reimplement tmember/2 as follows.

                tmember( Node, Tree ) :-
                    path( P, Tree ), 
                    member( Node, P ).

The following predicate gives the ``yield'' of a tree, that is, the list of leaf-labels, in order.

                yield( Label/[], [Label] ).
                yield( _/SubTrees, Yield ) :- 
                        SubTrees = [_|_],  % Not a leaf. 
                        yield_star( SubTrees, Yield ).
                
                yield_star( [], [] ).
                yield_star( [Next|Rest], Yield ) :- 
                        yield( Next, Y1 ), 
                        yield_star( Rest, Y2 ), 
                        append( Y1, Y2, Yield ).

This predicate represents a postorder traversal of the tree. The yields of the subtrees are determined, and then the yield of the current tree is determined as a function of those yields (i.e., their concatenation).

The final member of this family of predicates finds ``cuts'' through a tree. A cut---sometimes called a ``sentential form''---is a sequence of nodes (here identified with their labels) which taken all together dominate the entire string, and none of which dominate any of the others. Given a grammar and a rewriting system, the sentential forms are all those strings of terminals and nonterminals that one can get by rewriting the start symbol. One sees immediately that the yield of a tree is just a special case of a cut which contains the labels of only leaf nodes. Alternatively, a cut is just the yield of a truncated version of the tree. Not surprisingly, then, the code for these two predicates is almost identical, differing mainly in that cut/2 is permitted to end its recursion before it reaches a leaf (and also in that the order of the arguments has been reversed).

                cut( [X], X/_ ). 
                cut( C, _/SubTrees ) :- 
                        SubTrees = [_|_],
                        cut_star( C, SubTrees ).                
                
                cut_star( [], [] ). 
                cut_star( C, [SubTree|Rest] ) :- 
                        cut( C1, SubTree ), 
                        cut_star( C2, Rest ), 
                        append( C1, C2, C ).

6.4 Tree Geometry

Trees, as we have defined them here, are largely made up out of the immediate dominance relation (symbolized by `/') and the immediate precedence relation (symbolized by `.', the list constructor). Often, however, we are interested in other relations that can hold among the nodes of a tree. One simple example is the remote dominance, or ancestor relation, which is the reflexive transitive closure of the immediate dominance (alias ``parent'') relation. That is, every node is an ancestor to itself, and one node is the ancestor of another if there is a chain of parent-links which connects them.

                ancestor( A, B, Tree ) :- 
                        subtree( A/ASubs, Tree ), 
                        subtree( B/_, A/ASubs ).

Unfolding the code for subtree/2, we can see that ancestor/3 could also be defined as follows.

                ancestor( A, A, A/_ ).  
                ancestor( A, B, A/ASubs ) :-  
                        member( MiddleT, ASubs ), 
                        subtree( B/_, MiddleT ).  
                ancestor( A, B, _/SubTrees ) :-    
                        member( MiddleT, SubTrees ), 
                        ancestor( A, B, MiddleT ).

Note that this is a generalization of the list predicate earlier/3 which can be defined in the same two ways.

                
                earlier1( A, B, List ) :- 
                        suffix( [A|ARest], List ), 
                        suffix( [B|_], ARest.
                 
                earlier2( A, A, [A|_] ). 
                earlier2( A, B, [A|ARest] ) :- 
                        member( B, ARest ).  
                earlier2( A, B, [_|Rest] ) :- 
                        earlier2( A, B, Rest ).

We can also re-re-implement ancestor/3 in terms of path/2.

                ancestor( Hi, Lo, Tree ) :-
                    path( P, Tree ), 
                    earlier( Hi, Lo, P ).

The ancestor/3 relation is a partial order. That is, it is a relation which is (a) reflexive (A is an ancestor of A), (b) transitive (if A is an ancestor of B and B is an ancestor of C, then A is an ancestor of C), and (c) antisymmetric (if A is an ancestor of B and B is an ancestor of A, then A equals B). The first two conditions are built into the definition in a transparent manner. Antisymmetry follows, but the demonstration is a little more devious, and is clearest if we consider the first definition of ancestor/3.

If we can extend the immediate dominance relation to a partial order, then we ought to be able to extend the immediate precedence relation to a partial order as well. However, this is not quite as straightforward as the definition of ancestor/3. Essentially, A precedes B if we can climb up the tree from A and climb up the tree from B and eventually reach a point at which some ancestor of A and some ancestor of B are both daughters of the same node. Then, if A's ancestor is earlier than B's ancestor, A precedes B.

  precedes( A, B, Tree ) :- 
      Tree = _/SubTrees,
      earlier( ATree, BTree, SubTrees ),
      tmember( A, ATree ),
      tmember( B, BTree ).

We can also implement precedes/3 using cut/2, in the same way we used path/2 to reimplement ancestor/3:

  precedes( A, B, Tree ) :- 
      cut( C, Tree ), 
      earlier( A, B, C ).

This document was translated from L^AT_EX by H^EV^EA.

preorder	---	process the root,
		then the left subtree,
		then the right subtree;
inorder	---	process the left subtree,
		then the root,
		then the right subtree;
postorder	---	process the left subtree,
		then the right subtree,
		then the root.