Chapter 3 Elements of Prolog: Expressions, Unification, and Resolution

Prolog is a particularly simple programming language. It consists of a single data structure (which we will refer to here as expression trees) and a single operation on those data structures (called unification). The deductive calculus that it implements is equally simple. There is one inference rule (resolution) and no axioms. Despite all this it is an extremely powerful programming language. It can be used to implement Turing Machines, or theorem provers for full First-Order Logic, or Prolog itself, for example.

3.1 Proplog: The Resolution Rule for Propostional Logic Programs

We will introduce the Resolution Rule first for a strictly propositional version of Prolog, called Proplog. Essentially, Proplog is a subset of full propositional (or ``sentential'') logic in the same way that Prolog is a subset of full first order predicate logic. We cannot do very much with Proplog, but since we do not have to deal with variables, we can introduce the Resolution Rule independently of the Unification Operation. Then, at the end of the chapter, we put them together and arrive at (pure) Prolog.

3.1.1 Clausal Form

Proplog (and Prolog) programs are written in a special format called clausal form, which we now proceed to define, for the case of propositional logic. Formally, we take a clause to be an expression of the form:

A₁,...,A_m ¬ B₁,...,B_n,

where each of the As and Bs stand for propositions. A clause is meant to express a logical implication of the following sort: if all of the Bs are true, then one of the As must be true as well. This rule, which provides a semantics for clauses, is also true of the (classical propositional logic) expression

B₁Ù...Ù B_n ® A₁Ú...Ú A_m

The two expressions are equivalent, they mean the same thing. Here is yet another way of putting the same rule of interpretation: either at least one of the Bs is false or at least one of the As is true.

The following two laws of propositional logic

(p Þ q) º (¬ p Ú q)

¬(p Ù q) º (¬ p Ú ¬ q)

tell us that clauses are also equivalent to expressions of the form

A₁Ú...Ú A_mÚ¬ B₁Ú...Ú¬ B_n.

This version of the logic of clauses gives rise to yet another way of representing them:

{A₁,...,A_m,¬ B₁, ..., ¬ B_n }.

The elements of such sets are called literals, and the set is interpreted disjunctively. In the literature on logic programming and theorem proving you will see clauses represented in all of these (equivalent!) ways.

Given this interpretation (these interpretations?), the clause

A₁,..., A_m ¬

must mean that the disjunction of the As (A₁Ú...Ú A_m) is true, since it is impossible for one of the Bs to be false (there are none!). Also, the clause

¬ B₁,...,B_n

means that the conjunction of the Bs (B₁Ù...Ù B_n) is false, since it is impossible for one of the As to be true.

The empty clause ``¬ '' (also written \Box) therefore ought to mean something like ``true implies false,'' which is of course false. Therefore the empty clause is always interpreted as false.

The importance of clausal form is that we can do away with all the boolean connectives and, in the case of predicate logic, we can do without representing quantifiers as well. This way we don't need special rules to handle them all. Since the axioms of a standard logic are for the most part just there to tell us how to manipulate the connectives and quantifiers, needing no connectives means that we need no axioms, either. Nonetheless we don't lose anything (except succinctness!) by writing in clausal form. Every sentence of propositional logic has a translation into a set of clauses which is logically equivalent to it. (And the same remains true in the full first order case as well.) As a typical example that we will often encounter, the implication A₁ Ú A₂ Þ B can be represented by the set of clauses {(B¬ A₁), (B¬ A₂) }.

A Horn clause is a clause with at most one expression on the left of the arrow. The expression on the left of the arrow (if there is one) is called the head of the clause. The expression(s) to the right of the arrow (if there are any) make up the body of the clause. The four possible types of Horn clause are conventionally named as follows.

Facts
Clauses of the form A¬ . (Facts have a head but no body.)
Rules
Clauses of the form A¬ B₁,...,B_n. (Rules have both a head and a body.)
Goals
Clauses of the form ¬ B₁,...,B_n . (Goals have a body, but no head.)
Empty Clause
The clause \Box, with no head and no body.

A definite clause is a clause with exactly one expression on the left of the arrow, i.e., either a fact or a rule. A definite clause program or definite clause theory is a set of definite clauses. Prolog programs (and so, a fortiori, Proplog programs) are definite clause programs.

Clauses are represented in Prolog (usually) using ``Edinburgh'' syntax.

Facts
A.
Rules
A :- B1,...,Bn.
Goals
?- B1,...,Bn.

Figure 3.1: Clausal form, Edinburgh style

Observe that all clauses end in a period. Note that the `?-' symbol is the Prolog intepreter's prompt, so you don't ever type that in yourself. You should have no need to ever type in the empty clause. Note that (at least in SICStus Prolog) the expression ``?-.'' (got by typing a period at the Prolog interpreter's prompt) will cause an error.

3.1.2 The Resolution Rule and the Interpretation of Logic Programs: The Propositional Case

The resolution rule was originally developed for use in full First-Order Logic theorem provers. Prolog uses a very specialized form of resolution (called ``SLD Resolution'') specifically adapted to definite clause programs, so I will not present a general introduction to resolution systems here.

The fundamental operation of a resolution system takes a pair of clauses as input and produces a new clause, called their resolvent as output.

In a Prolog computation we are given a program which, as we already know, is a set of definite clauses, and we are also given a single goal clause which expresses the particular problem instance we wish to solve. In the kind of resolution implemented in Prolog, one of the two clauses we resolve must always be the goal clause, and the resolvent always becomes the new goal clause. This is called linear resolution.

The resolution step then proceeds as follows. First, we take the current goal clause and we select one of its constituent atoms. In principle, we can select any atom we want, but Prolog will always select the leftmost member of the goal clause. This is called resolution with a selection function. Prolog's selection function applies to a sequence of expressions and returns the leftmost expression in that sequence. This sort of resolution system is called linear resolution with selection function, or SL-resolution. Therefore you will often see Prolog's particular type of resolution called SLD-resolution, with the `D' standing for `Definite Clauses'. The variant of resolution we will use for Proplog is just SLD resolution further restricted to clauses where all the atoms are propositions.

Our second step, after selecting an expression from the current goal clause, is to search the program for a clause whose head matches the selected sub-goal. In Prolog (and so also in Proplog), this search follows the order in which clauses appear in the program text. In the propositional case, the resolvent of the goal with the clause we select is the result of (a) removing the selected member of the goal clause and (b) replacing it with the body of the selected program clause.

Given: A goal clause ¬ G₁,...,G_k
Search the program for a program clause A ¬ B₁,...,B_n such that G₁ matches A . If no such clause exists, then fail.
Replace G₁ with B₁,...,B_n .
If the result is the empty clause, then halt, reporting success.

Figure 3.2: Proplog's version of the Resolution Rule

Note that if we resolve the goal with a fact, then we replace it with nothing (since facts are clauses without bodies). That is, we simply remove it from the goal. Intuitively, when the goal finally becomes empty, then we know we have reduced our original goal to a collection of facts, and so we have proved the original goal. This intuitive presentation of the declarative interpretation of logic programs under the SLD Resolution Rule is in fact not quite accurate, but it will do for the purpose of gaining reliable intuitions about how Prolog programs should be interpreted. For the reader interested in more details of the logic underlying (propositional) resolution, we offer the following subsection, which can be skipped if desired.

A Brief Introduction to Propositional Resolution

The careful reader may have noticed that in our presentation of the types of Horn clause we referred to clauses like ``¬ A₁,...,A_m '' as goal clauses. However, when we were talking about the interpretation of clauses, we observed that such a clause is equivalent to the negation ¬( A₁ Ù ··· Ù A_m ) . If our intuitive goal is to prove A₁ Ù ··· Ù A_m , why do we refer to the negation of that expression as the ``goal clause''?

The answer is that resolution-based theorem-provers are refutation provers. Recall the definition of logical consequence. Given a program (a set of clauses) P, a clause G is a consequence of P just in case every interpretation which satisfies P also satisfies G. Notice that if this is true, that every satisfying interpretation of P also satisfies G, then there can be no satisfying interpretation of P which satisfies ¬ G. If there were, then there would be a way of interpreting P which satisfied GÙ¬ G , which is a contradiction. Note further that if no satisfying interpretation of P also satisfies ¬ G , then there exists no satisfying interpretation of P È {¬ G }. So one way to prove that G is a consequence of P is to prove that P È {¬ G } is unsatisfiable. This is called a proof by refutation. To prove something, you refute its contrary.

Sometimes it is easier to prove that sets of logical sentences are satisfiable, sometimes it is easier to prove that they are unsatisfiable. In the latter case, refutation methods are obviously useful, and that is the situation we are in with computational logic. As a result most automated theorem proving methods are based on refutation.

In the particular case where all our sentences are in clausal form, we can implement a refutation theorem prover in the following way. We know that the empty clause, \Box, is unsatisfiable. Suppose then that we had an inference rule which was sound, that is, which was such that if its inputs were satisfiable, its output would be too. Suppose further that we apply this inference rule to a program P and a negated goal ¬ G, and eventually derive \Box. It is a law of logic that, if A implies B, and furthermore B is false, i.e., ¬ B is true, then A must be false. By the soundness of our inference rule we have that, if the inputs are satisfiable (A), then the output is satisfiable (B), and by the fact that the output is \Box we have also ¬ B. Therefore the claim A, that the inputs were satisfiable, must be false: the inputs were in fact unsatisfiable. By an induction on the length of the proof, we work our way back to the realization that our original assumptions, taken together, must be unsatisfiable. That is, P È {¬ G } is unsatisfiable, that is, there is no interpretation of P which makes ¬ G true, that is, every interpretation of P makes G true, that is, G is a consequence of P.

The final piece of the puzzle, then, is to show that the Resolution Rule is indeed sound. For general propositional resolution, we can represent the rule as:

{A₁,...,A_i, X, A_i+1,...,A_m } {B₁,...,B_j, ¬ X, B_j+1,..., B_n }

{A₁,..., A_m, B₁, ... B_n }

To prove soundness we assume that the inputs are satisfiable and show that, under that assumption, the output must be as well. Assume that the boolean valuation v is one of the interpretations which make the inputs true. Then v either makes X true or it makes it false. Assume for the moment that it makes X true. By assumption, v also makes the second input clause (call it B) true. But if it makes X true, it must make ¬ X false, so in order to make B true, it must make one of the other literals in B true (call it B_k). Since B_k is not ¬ X, it must be a member of the output clause. So we know that, under v, the output clause must be satisfiable, because it contains a literal that v makes true. The other half of the proof, under the assumption that v makes X false, is entirely symmetrical, and we leave it as an exercise to the reader.

We can also show that the Resolution Rule is complete, which means that if the output is satisfiable, then the inputs must have been as well. That means that if we can't derive \Box from P È {¬ G } then G must not be a consequence of P. That proof is more complex, however, and less important for building confidence in the declarative interpretation of Prolog programs. So we leave it out, and refer the reader to Melvin Fitting's excellent and very useful book First-Order Logic and Automated Theorem Proving (Springer, 1990).

3.1.3 An Example of Proplog in Action

We will illustrate the resolution rule with the simple theory in propositional logic given in table 3.3. We use ``Edinburgh syntax'' here---refer back to table 3.1 if necessary.

s :- np, vp.
s :- np, aux, vp.

np :- det, n.   np :- name.

det :- the.     det :- every.

n :- prisoner.

% No clauses for name.

aux :- has.    

vp :- v.        

v :- escaped.

% Lexicon:
the.   every.
prisoner.   
has.
escaped.

Figure 3.3: A Proplog Theory.

This theory looks a lot like a phrase structure grammar, but note that it means something a little funny, since it just treats what we think of as grammatical categories as if they were simply facts. So all we can really do is establish whether or not s is a true fact. Roughly, the lexicon is a collection of facts and the program can tell us whether or not these facts can be combined in such a way as to make an s or a vp, for example. So ultimately the only interesting questions we can ask are questions like ``Are there any S's,'' or ``Are there any NP's.'' We cannot, for example, find out what those S's and NP's actually are. Still, it makes a good starting place: the subject matter is familiar, and the form is simple.

Suppose then that our initial goal is the query ``?- s.'' We apply our selection function to select an atom from the goal. The leftmost atom in the goal is, of course, s. Then we search the program for clauses whose heads are s. There are two of them:

s :- np, vp.
s :- np, aux, vp.

According to our Prolog-style implementation of the Resolution Rule, we must try the first clause first. So we store some indication that we have not yet tried clause 2 (this is usually called a ``choice point''), and we remove the atom s from the goal and replace it with the body of the first clause, giving the new goal ``?- np, vp.''

Now the cycle repeats itself. We apply the selection function to the goal, yielding np. We search the program for clauses headed by np, finding now

np :- det, n.
np :- pron.
np :- name.

We start with the first clause, as always. So we push a new choice point onto the stack, recording that clauses 2 and 3 remain untried, and we replace the selected atom in the goal with the body of the selected clause, yielding the new goal ``?- det, n, vp.'' We select det next, pick the first clause in its definition, and replace it in the goal with the body of that clause, yielding the new goal ``?- the, n, vp.'' We select the, pick the first and only clause in its definition and replace it in the goal with the body of its clause. The body of its clause is empty, so the result of this ``replacement'' is ``?- n, vp.'' It should be clear from this point how the rest of the proof proceeds. We summarise it as follows.

?- s.
?- np, vp.
?- det, n, vp.
?- the, n, vp.
?- n, vp.
?- entity, vp.
?- vp.
?- v.
?- exists.
?- .

In the last step we derive the empty clause, so the original goal succeeds.

Just as the program looks a lot like a context-free phrase-structure grammar, so this proof looks a lot like a derivation from that grammar. The only real difference is that we throw away the terminal categories the, entity, and exists, rather than glueing them together into a string. We will see later how to capitalize on this correspondence between definite clause proofs and phrase structure derivations to develop an extremely powerful grammar formalism, known as Definite Clause Grammars (DCGs). For the moment, however, we are just trying to understand how the Resolution Rule, as implemented in Prolog, works.

Backtracking

Our previous proof went very smoothly. What happens when things go wrong? Suppose, for example, that we changed the definition of np to the following.

np :- name.
np :- det, n.
np :- pron.

All we have done here is to reorder the clauses so that the one defining noun phrases as names (i.e., proper nouns) comes first. Observe that there are no clauses in the definition of name. So the derivation does not proceed very far. We give the first few steps of the derivation below, together with the choice points we create; we represent choice points here as pairs of the form (<selected-atom>,<next-untried-clause>), and write them so that the leftmost choice-point is always the most recent.

Goal:               Choice Point Stack:
?- s.               
?- np, vp.          (s,2)
?- name, n, vp.     (np,2),(s,2)

Now, the search for clauses defining name fails, so we have to backtrack. Backtracking just means that we pop the most recent choice-point off of the top of the stack, and go back to the point at which we selected that atom. In this example, the last choice we made was which clause to resolve np against, and the next untried clause is clause number two. So we choose that clause, and replace np with det, n. Now the proof looks as follows:

Goal:               Choice Point Stack:
?- s.               
?- np, vp.          (s,2)
?- name, n, vp.     (np,2),(s,2)
<fail; backtrack!>
?- np, vp.          (s,2)
?- det, n, vp.      (np,3),(s,2)

Now the proof continues as in the first example.

What if the definition of np had consisted only of the single clause ``np:- name.''? There are no more clauses to try, so there is no reason to push a choice-point.

Goal:               Choice Point Stack:
?- s.               
?- np, vp.          (s,2)
?- name, n, vp.     (s,2)

So, on backtracking, we would go all the way back to the s-rule, to try its second clause. Of course, in this grammar every sentence requires an NP, so there is ultimately no way past this faulty np-rule! In this case we will ultimately run out of choices and, at some point, the proof will fail and the choice point stack will be empty. At that point, Prolog finally admits failure, and prints out the rather uninformative answer ``no''.

Proof Trees and Search Trees

A tool which is often useful in the design and analysis of logic programs is the proof tree. Intuitively, a proof tree just records the successful proof of a goal in tree-like form. A little more formally, if we think of arbitrary Proplog clauses as grammar rules, then proof trees are just the trees generated by that ``grammar''. And when a Proplog program (a ``propgram''?) really does represent a grammar then, well, the resemblence between proofs and derivations becomes that much more obvious.

Figure 3.4:

The proof tree in figure 3.4 can be read as follows. In order to prove s we had to prove np and we had to prove vp. To prove np we had to prove det and n. To prove det, we had to prove the, and the proof of the was immediate from the program.

Proof trees can be very helpful when you are designing a new program. They help one to reason about a problem in terms of its subproblems: in order to prove my overall goal, what things do I need to accomplish first? The tree shape reminds one that, once one knows that np must be established, the problem of how to do so can be solved in a similar fashion, and in isolation from other problems, like how to prove vp.

A proof tree is read conjunctively: a parent node is established by establishing its first daughter, and its second daughter, and so forth. This focuses attention on what logical resources are required in order to prove a goal. However, it does not tell us what gets done with other resources in our program. That is, the proof tree focuses on a successful proof, and describes how that proof went, but it abstracts away from all the searching the Prolog engine might have had to do to find that proof. To give us a better idea of how much work the Prolog engine has to do we use search trees.

Search trees are read disjunctively. Nodes are labeled with goals, and each daughter node represents one way of attempting to prove the goal labeling its parent node. The shape of a search tree depends very heavily not only on the program but also on the interpreter that runs it. In particular, we can only draw a search tree once we know the selection function our interpreter uses. Since Prolog uses a leftmost-first selection function, we develop a search tree as follows. Given a node labeled with the goal ?-G1,...,Gn. we search the program for clauses whose heads match G1 and, for each such clause, we give our node a daughter labeled with the resolvent of the parent goal with that clause. That is, we replace G1 with the body of the clause we have found.

Figure 3.5:

The tree in figure 3.5 shows most of the search tree for the goal ?-s., given the program in table 3.3. (For the most part the missing pieces are just copies of parts of the search tree given in the figure.) We have ordered daughter nodes from left to right so as to reflect the order of clauses in the program. Accordingly, Prolog can be seen as executing a depth-first, left-to-right search of the search tree, looking for leaf nodes labeled ``Success'' (i.e., looking for instances of the empty clause). If we reorder the clauses in the program so as to force backtracking, and reorder the subtrees of the search tree accordingly, we move the branch that ends in ``Failure'' to the left of the success branch. Prolog's backtracking can now be seen as just climbing back up the search tree to the most recent branching node and trying another daughter of that node until it runs out of daughters to try; then it must climb back up a little higher. In this way, Prolog will eventually search the entire tree if it has to, and if it finds no success-nodes, then it will report failure and halt. That is, it will halt as long as the search tree is finite. If the search tree is infinite, well then, things are a little more complicated, as we see in the next section.

Left Recursion and Infinite Proof Searches

There are two famous problems that can arise due to compromises that were made in the design of Prolog. One of them is as follows. I asserted of the program with the faulty np-rule that at some point Prolog will run out of choices. However, there are programs for which Prolog will never, ever run out of choices. Often this is not a problem: it just means there are an infinite number of distinct solutions, and if you want them all you must have infinite patience! But sometimes this means that an otherwise logically correct program, given a true goal with a finite number of distinct answers will nonetheless fail to halt. Suppose we add the following clause to the s-rule.

s :- s, and, s.

We add ``and.'' to the lexicon as well. Now, given the faulty np-rule, we will ultimately have to use this new clause and expand the goal ``?- s.'' to ``?- s, and, s.'' Ultimately, the other two clauses for s will fail again, for lack of any proofs of np, and we will work our way down to clause 3 of s again, expanding the goal to ``?- s, and, s, and, s. Every time we expand ``s'' to ``s, and, s'' we get a whole new fresh set of choices for how to expand the leftmost literal. Clearly this program will never halt: it will even fail to fail. In terms of search trees, the search tree for this goal now contains an infinite branch.

The problem is that we have a rule in our program which is left recursive: it calls itself first, before it does anything else. Left recursive programs will (almost) always eventually fall into an infinite proof-search. This is a severe problem, but it can be remedied. It is always possible to convert a left recursive program into an equivalent, non-left-recursive program, but the result is not always so readable. In our case we could redefine the grammar so that it contains a new non-terminal symbol, called foo, and redefine s as follows.

s :- foo.
s :- foo, and, s.

foo :- np, vp.
foo :- np, aux, vp.

What we have done is to package all of the unproblematic s-rules from the old grammar under the new symbol foo. Now the s-rule will only call itself after it has found a foo. In our example with the faulty np-rule, we are guaranteed to run out of ways to prove foo, and, failing to find a proof for foo, we will not look for further ways to prove s.

The solution works, but at some cost: in our case, we have introduced a symbol which has no part to play in our theory of grammar. It is meaningless; or rather, it only has a procedural meaning. As a result, our proofs are no longer identical to derivations in the corresponding grammar. Even worse is the following. Normally a sentence of the form ``S and S and S and S,'' can have a number of interpretations, corresponding to the bracketings [S and [S and [S and S]]], [[S and S] and [S and S]], and so on. Our modified program will find only one way to prove that such a sentence is an s, corresponding to the first of these bracketings. These problems can be gotten around, but the example still serves to show that, even when efficiency is not a concern, we still have to know something about Prolog's procedural interpretation just to get our programs to halt. Efficiency may not be a concern at the moment, but effectiveness always is.

3.2 The Unification Operation

3.2.1 Expressions---A universal data structure

Prolog is designed for symbolic computations; in this it is very different from a language like Fortran which is designed specifically for numeric computations. We begin by assuming that we have available to us a large collection of unanalyzable primitive expressions, or just ``primitives'', for short, corresponding to a sort of alphabet or lexicon. Out of these we will construct larger and larger expressions which we can use in various ways: as names for things, relations on the things so named, sentences about these relations, and finally sets of such sentences. These logical objects will then be shown to correspond to familiar programming constructs along the following lines.

terms (i.e., names)	«	data structures
relations	«	procedure and function calls
sentences	«	procedure definitions
sets of sentences	«	programs

Our primitives come in three basic flavors, or types: variables, numeric constants, and symbolic constants. The type of a given primitive is determined by the following naming conventions.

Variables

Variables are written as strings composed of

letters,
numbers, and
the underscore character (_)

beginning with either

an uppercase letter, or
the underscore character.

For example, X, X1, NP_Tree, _the_weather are all legal variables.

Constants

Numerals

Okay, you all know what those look like...

Symbols

Symbol names are either

`standard' symbols: which are composed the same way as variable names, except that they begin with a lowercase letter, or
operator symbols: which are for the most part predefined (for example, <, =, +, ->, :-, \+, etc.)
quoted symbols: that is, arbitrary strings enclosed in single quotes.

For example, a, a31, death_and_taxes are all legal names for symbolic constants.

From these primitive symbols we construct expression trees according to the following recursive definition.

A single node labeled with either a constant or a variable is an expression tree.
A tree whose root is labeled with a symbol and whose subtrees are all expression trees is an expresison tree.
Nothing else is an expression tree.

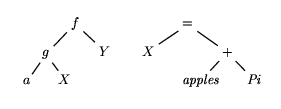
Figure 3.6: Some expression trees, written ``horizontally'' as f(g(a,X),Y) and X=apples+Pi.

Concretely, we write these expression trees in one of two ways. If the root is labeled with a standard symbol or a quoted symbol, then we write

ároot-labelñ(ásub-tree-1ñ,...,ásub-tree-nñ).

For example, f(g(a,X),Y) is a way of writing the expression tree whose root is f and whose subtrees are the expression trees which we write as g(a,X) and Y (see figure 3.6). Operators, on the other hand, are written infix when they take two arguments and are written either prefix or postfix, depending on the operator, when they take only one argument. For example, X = apples + Pi is a way of writing the expression tree whose root is labeled `= ' and whose subtrees are the expression trees X and apples+Pi . As usual, we can (and sometimes we must!) use parentheses to make it clear what the structure of the expression tree is. For example, the following are all correctly written expression trees.

ancestor( X, eve )

head(NounPhrase,Noun)

Current_Product * 2

3 * (4+2)

The reason for focusing on the more abstract notion of expression tree rather than the concrete expressions illustrated above is that we can abstract away from the different ways of writing expression trees, and focus on their structure, no matter how it may happen to be written down.

3.2.2 Unifying Expression Trees

Now that we have some data structures we can work with, let us investigate what we can do with them. We ask first perhaps the most elementary question we can imagine: When are two data structures equal? We will ask this question under particularly strict conditions: When is it valid to claim that two expression trees are equal?

Validity means that a claim holds under all the possible (logical) ways of interpreting the symbols it contains. Consider for example the following claim.

2 + 2 = 4

Now, numerals like 2 and 4 and operations like + have certain very popular, very traditional interpretations, and under these interpretations, both the expression 2+2 and the expression 4 denote the same number. However, to paraphrase Humpty Dumpty in Through the Looking Glass, which is to be the master, you or the symbol?

``When I use a word,'' Humpty Dumpty said in a rather a scornful tone, ``it means just what I choose it to mean--neither more nor less.''

``The question is,'' said Alice, ``whether you can make words mean different things.''

``The question is,'' said Humpty Dumpty, ``which is to be master---that's all.''

For example, there is no mathematical or logical difficulty in interpreting `2' and `4' as themselves, i.e., as one-character strings, and interpreting `+' as the concatenation operator, in which case `2 + 2 ' is another name for the string `22', which is certainly not the same string as `4'.

So let us ask ourselves under what conditions a given equation is valid? The answer is quite simple: when both sides are syntactically identical. Clearly, for example,

2+2 = 2+2

will be true no matter how we interpret `2' or `+'. (Equality, in first-order logic, has a fixed interpretation: we don't get to play around with that!) This is the kind of equality which Prolog uses: syntactic equality. The advantage of this is that from it we can get back any more permissive interpretation we might want. For example, it is a relatively simple matter to define a predicate arithmetic_value or a predicate string_value in Prolog such that arithmetic_value(2+2,4) is true and string_value(2+2,22) is true. Note that it would be rather more complicated to implement the string interpretation if our basic interpretation of our symbols was the standard arithmetical one.

Now let us grant ourselves some variables, to represent unknown information. A fundamental question in logic programming is a question like the following (written Edinburgh-style).

?- 2+X = Y+3.

This particular goal is interpreted as meaning ``for what values of X and Y is this goal valid?'' The answer is that it is a valid claim about expressions only as long as X=3 and Y=2. Only then are the expressions on either side of the equality syntactically equal.

Two expressions that can be made syntactically equal are said to unify, and so goals like that above are often termed unification problems. The set of variable bindings {X=2,Y=3}(more often written {X/2,Y/3}) is called a unifier for the given pair of expressions. We can very fruitfully think of this unification problem as expressing a certain kind of constraint on the values of the unknowns X and Y. Note that the solution to the original equation is itself a set of equations. It is a set of equations of a very special sort, namely one in which the left hand side is always a variable and furthermore it is a variable which appears nowhere else in the set of equations. (Most especially, it does not appear on the right hand side of its own equation.) Such a set of equations is said to be in solved form: it is a constraint satisfaction problem which ``wears its solution on its sleeve,'' so to speak. The unification operation is essentially a process of converting an arbitrary set of equations into a set in solved form (if that is possible).

Consider now a unification problem with a less restricted set of solutions.

?- tree(s,NP,VP)=tree(Parent,john,Predicate).

Clearly Parent must equal s and NP must equal john to solve this equation, but what are we to do with VP and Predicate? Clearly we can assign any expression to VP as long as we assign the same expression to Predicate. There are an infinite number of distinct expression trees, so this problem has an infinite number of solutions. However, no matter what those solutions are, they satisfy the simple equation VP=Predicate. The solution {Parent=s, NP=john, VP=Predicate}is indeed a solution---it is in solved form---and furthermore it is a most general solution, or ``most general unifier'' (mgu, for short). Typically, mgu's are not unique (in this example we could have said {Predicate=VP}instead, for example). However, all mgu's for a given problem are isomorphic; they differ only in the names of the variables. So we usually speak of ``the'' mgu for a problem and say that, if it exists, it is unique (up to isomorphism).

These same ideas can be applied to sets of equations, not just single equations. We usually speak of ``systems'' of equations in this case. Like single equations, systems of equations also have a (unique) most general unifier. Consider, for example, how we might intuitively go about solving the following system of equations.

?- T=tree(s,NP,VP), T=tree(Root1,john,Pred), 
   T=tree(Root2,Subj,sneezes).

Here we have three different constraints on the value of T, for which we must find a single solution. One thing we can do, since we know that among other things T=tree(s,NP,VP), we can substitute the expression on the right for T in the original system. We transform it to the following, equivalent system.

?- T=tree(s,NP,VP), tree(s,NP,VP)=tree(Root1,john,Pred), 
   tree(s,NP,VP)=tree(Root2,Subj,sneezes).

Clearly, this system has the same solutions as the original: all we have done is to substitute equals for equals. In other words, we have eliminated the variable T from the system of equations. (Note that we have not literally ``eliminated'' it: it still appears once on the left hand side of the first equation. Nonetheless, it will play no further role in our calculations.)

Now, if we are to solve the second member of this system,

tree(s,NP,VP)=tree(Root1,john,Pred),

then it will have to be the case that the following three equations are satisfied.

Root1=s, NP=john, VP=Pred.

In general, two structures can only be equal, under the theory of syntactic equality, if their functors are the same (tree, in this case), they have the same number of arguments (3, in this case), and each of the arguments is equal. So we decompose a more complex unification problem---the problem of unifying two structures---into several smaller ones---the problems of unifying the argument-pairs.

We are now looking at the following system.

?- T=tree(s,NP,VP), Root1=s, NP=john, VP=Pred,
   tree(s,NP,VP)=tree(Root2,Subj,sneezes).

One thing we can do now is to ``eliminate'' the variables NP and VP.

?- T=tree(s,john,Pred), Root1=s, NP=john, VP=Pred,
   tree(s,john,Pred)=tree(Root2,Subj,sneezes).

Next, we can decompose the last equation.

?- T=tree(s,john,Pred), Root1=s, NP=john, VP=Pred,
   Root2=s, Subj=john, Pred=sneezes.

Finally, we can do variable elimination on Pred.

?- T=tree(s,john,sneezes), Root1=s, NP=john, VP=sneezes,
   Root2=s, Subj=john, Pred=sneezes.

This system is in solved form; it is the most general unifier for the original system. We find, after all that work, that there is just one value possible for T in the most general unifier.

In general, we can characterize the unification operation as the transformation of a system of equations into a system in solved form, using the following three rules.

Trivial:

{u=u }È S ¾® S.

Term Decomposition:

{f(u₁,...,u_n)=f(v₁,...,v_n)}È S ¾® {u₁=v₁,...,u_n=v_n }È S.

Variable Elimination:

{x=v }È S ¾® {x=v }È s(S),
where x=v is not in solved form, x does not occur in v, and s is a function replacing every occurrence of x in S with v (the substitution of v for x in S).

Figure 3.7: Rules for solving unification problems.

We will find, once we put unification and resolution together to yield Prolog, that Prolog programs typically generate very large systems of equations to solve. The user generally has a much narrower view of what the problem of interest is, namely the original goal that s/he input. So Prolog does not output the entire solved form of the entire system of equations it has solved. Instead it just prints out the bindings of the variables which appeared in the original goal.

Systems of equations in solved form can be thought of equivalently as defining functions from variables appearing on the left of the equations to the expressions occurring on the right. So we can apply a unifier to an expression (as we do in the definition of variable elimination). We refer to such functions as substitutions, and we write them as postfix operators. So, if q is the substitution function defined by some solved system of equations, then we may write Eq for the result of applying q to an expression E.

Here are some examples of pairs of expressions, their mgu's (thought of now as substitution functions and written using the Variable/Value notation), and the result of applying the mgu to the expressions.

f(X) , f(f(Y)) , s = {X/f(Y)},
f(X)s = f(f(Y))s = f(f(Y))
0 + X , N + 1 , s = {N/0, X/1},
(0+X)s = (N+1)s = (0+1)
apply(f,a,Term) , apply(f,Arg,f(Arg)) ,
s = {Arg/a,Term/f(a) },
apply(f,a,Term)s = apply(f,Y,f(a))s = apply(f,a,f(a))

The following pairs of expressions do not unify.

a , f(X) : a and f are not identical symbols.
X , f(X) : ``occurs-check'' violation---X occurs in its own value.
f(X) , f(X,Y) : nothing to unify Y with.

3.3 Prolog: Resolution with Unification

3.3.1 The language of First Order Logic

First-order logic uses expressions, roughly as we have defined them here, to play two distinct roles: as names for individuals (terms) and as statements of relations holding among individuals (formulas). At a certain level, there is no formal difference between terms and formulas. As data structures they are identical: they are all instances of expression trees. So, for example, it is possible to unify two expressions regardless of whether they are both terms or both formulas. However there is in first order logic a crucial semantic difference between them. For example, the term 2 * 2 combines two numbers to yield another number. It has a definite value; in fact, we can think of 2*2 as just another name for 4. Or, to be excruciatingly precise, both 2*2 and 4 (and ``four'') are names for some number which, of course, we cannot speak of without naming it one way or another. On the other hand, a formula like even(4) (equivalently even(2*2)) does not name another number. In this case it names a property, or rather, states a claim that that property (the property of being even, or divisible by 2) holds of (the number denoted by) 4.

So, in defining a first-order language to express a particular problem of interest, solutions to the problem, and proofs of the solutions, we begin by sorting our heap of primitive expressions into two distinct piles: predicate-names and function-names. Furthermore we associate with each symbol a number, called its arity, which indicates how many arguments it combines with to form a well-formed expression of the appropriate sort. A collection of symbols sorted this way is often called a ranked alphabet or a signature. Concretely, when presenting a signature we will write function and predicate names followed by their arities as, e.g., f/2. Keep in mind that f/1, the one-place function or predicate symbol, is (logically speaking) a different symbol from f/2.

Note that we will usually refer to function names with zero arity as ``constant terms'' or just ``constants.'' Note also that we do not consider variables as part of the signature; we always assume that we have as many of them as we need, and so there is no need to name them in advance, and they never take arguments (in first order logic), so there is no need to assign them arities.

The rules of our syntax are as follows. From the symbols in our signature, together with a collection of variables, we will construct terms. Terms are expression trees whose roots are labeled with variable names, constant names or function names, and which have exactly the number of daughters specified by the root's arity. (So variables and constant terms, having zero arity, will have no subexpressions.) Each subterm must also be a term.

A term T is an expression satisfying one of the following conditions:

T is a variable;
T is a constant-name, that is, a function-symbol of arity 0.
T is an expression-tree whose root is labeled by a function-symbol f, with arity n, with exactly n subexpressions, each of which is itself a term.

Given a signature in which s is a function symbol of arity 1 and 0 is a constant, 0 , s(0) , and s(s(0)) are all terms. s(0) has a single subterm, 0 , and s(s(0)) likewise has a single subterm, s(0) . Terms are interpreted as names for things. Suppose, for the moment, that we want to be able to talk about natural numbers and elementary arithmetic, so we want our terms to name numbers. So, for example, we intend that s(0) name the number one (i.e., the successor of the number zero). As noted, first order logic is distinguished from higher order logics in requiring that variables all have zero arity. So X is a term, but X(0) is not any sort of well-formed expression of first order logic. (If you try and type it into the Prolog interpreter, you will get an error message!)

From terms we can go on to define atomic formulas as follows.

An atomic formula is an expression tree whose root is a predicate-symbol p of arity n, with exactly n subexpressions each of which is a term.

This sounds a lot like the definition of a term! Note, however, that terms are defined recursively (a term is made out of other terms), but atomic formulas are not (an atomic formula is not made out of other atomic formulas).

In standard first-order logic, we would go on to define well-formed formulas as collections of atomic formulas bound together by the connectives Ù , Þ , etc. and attached under the quantifiers " and $ . For example,

" X ($ Y eq(X,s(Y)) Þ ¬ eq(X,0))

would be a formula of standard first order logic using our signature (with eq a predicate symbol of arity 2). However, as we already know, Prolog uses (part of) the logically equivalent, but formally different writing system of clausal form. In clausal form we do not represent the connectives and quantifiers directly, so I will not go into any further detail about the standard writing system of first order logic.

3.3.2 Clausal Form for Predicate Logic

In the case of the predicate calculus, a clause is still an expression of the form:

A₁,...,A_m ¬ B₁,...,B_n,

but now each of the As and Bs are atomic formulas. Beyond that, we just have to deal with the fact that the atomic formulas in predicate clauses can contain variables as subexpressions. In this case, the variables are treated as if they were all bound by universal quantifiers (" ) placed at the front of the clause. So, for example,

entity(X) ¬

means the same thing as the standard first order logic sentence

" X entity(X)

namely, ``for all X, X is an entity.'' Similarly, a clause like

mortal(X) ¬ human(X)

means the same thing as

" X (human(X) Þ mortal(X))

that is, ``for all X, if X is human then X is mortal,'' and the clause

¬ different_from_self(X)

has the same meaning as

" X ¬ different_from_self(X).

Note that " X ¬ f is equivalent to ¬ $ X f . (That is, ``for all X f does not hold,'' is equivalent to ``there is no X such that f holds.'') For this reason it is often useful to think of variables occurring only to the right of the arrow as being implicitly existentially bound. Accordingly, the following clause

ancestor(X,Y) ¬ parent(X,Z), ancestor(Z,Y)

can either be read as ``for all X, Y, Z , either X is an ancestor of Y or else Z is not a parent of X or else Z is not an ancestor of Y ,'' (its literal meaning) or it can be read as ``for all X, Y , X is an ancestor of Y if there is a Z such that X is a parent of Z and Z is an ancestor of Y .''

Just as our interpretation of propositional clauses allowed us to do away with connectives, our interpretation of predicate clauses allows us to do away with quantifiers.

The definitions of Horn clause, definite clause, rule, fact, goal and empty clause remain the same for predicate clauses. Proplog programs were sets of propositional definite clauses. Prolog programs are sets of (first-order) predicate definite clauses.

3.3.3 The Resolution Rule for Predicate Clauses

Just as with the definition of clauses, we do not change anything in the definition of the Resolution Rule except to add to it mechanisms to deal with variables.

We define first a renaming substitution: it is a substitution which simply maps variables to new variables. If we are considering a pair of clauses that we would like to resolve, we require that the set of variables they involve must not overlap; each must have its own separate set of variables. This is not really a very strong requirement, though, since if they both mention a variable named X we can just apply a renaming substitution to one of them. This is called naming apart, and after naming apart we call the pair of clauses separated. Resolution is only defined for a pair of separated clauses.

In defining resolution for predicate clauses, we now add a constraint pool, where we keep track of all of the unification problems we have solved. The constraint pool acts as an environment, telling us the current value of all of our variables. As before, the first step in the resolution process is to select an atom from the current goal. Our second step, after selecting an atom from the current goal clause, is to search the program for a clause whose head unifies with the selected sub-goal. (Note that this covers the case of ``matching'' atoms in the propositional subcase.) In the process of finding a clause whose head unifies with the currently selected atom, we will of course find the mgu for the clause-head and the goal-atom. The resolvent of the goal with the clause we select is the result of (a) removing the selected member of the goal clause, (b) replacing it with the body of the selected program clause, and (c) adding the mgu to the constraint pool. Note that high-performance Prologs do not usually bother to keep the constraint pool in solved form; in particular, variable elimination is not usually used. Given {X=Y, Y=a }, a Prolog interpreter can simply follow the obvious chain of inferences to get from X to its current value, a.

Interpreted as an environment or substitution giving the current values of all of our variables, we can think of step (c) alternatively as applying the substitution we have built up to the new goal. The point is, if we select an atom containing a variable X, and unify it against the head of some program clause, with the result that we now have new information about the value of X, we must keep in mind that that new information applies to every instance of X in the goal, not just in the selected atom.

As before, if we resolve the goal with a fact, then we remove the selected atom from the goal. Of course, unifying the selected atom with the fact may create new variable bindings which need to be added to the constraint pool.

A resolution derivation is just the repeated application of resolution steps. A resolution derivation succeeds just in case we eventually derive the empty clause. In that case, the solution of the original goal is the bindings for the variables that appeared in that goal taken from the final state of the constraint pool.

Given: A goal clause ¬ G₁,...,G_k and a constraint pool C.
Search the program for a (variant of a) program clause A ¬ B₁,...,B_n such that G₁ unifies with A with s as their most general unifier (mgu). If no such clause exists, then the resolution step fails.
Replace G₁ with B₁,...,B_n .
Replace C with the solved form of the system s È C . Thinking of s as a substitution function, the new goal equals
¬ (B₁,...,B_n,G₂,...,G_k)s

Figure 3.8: Prolog's version of the Resolution Rule

Suppose for example that we want to resolve the two clauses below. (The s-function is meant to be interpreted as the arithmetic successor function; that is, s(N) = N+1 .)

¬ plus(s(0),s(s(0)),X). (3.1)

plus(s(X),Y,s(Z)) ¬ plus(X,Y,Z). (3.2)

The clause in (3.1) is a goal clause, and the clause in (3.2) (a rule clause) is meant to come from a program defining addition for natural numbers. Note that clause (3.2) is indeed a true sentence about the natural numbers: if X+Y = Z , then certainly it is true that (X+1)+Y = Z+1 .

Keep in mind that we must name the clauses apart before we do anything else. (In particular, notice that the variable name X has gotten used in both clauses.) So in effect we are resolving the following two clauses.

	¬ plus(s(0),s(s(0)),X₁).
	plus(s(X₂),Y₂,s(Z₂)) ¬ plus(X₂,Y₂,Z₂).

There is only one member of the goal clause (3.3), so we select that. It does indeed unify with the head of the program clause (3.4). Their mgu is

{X₁=s(Z₂), X₂=0, Y₂=s(s(0)) },

and this becomes the value of our current environment. Therefore our resolvent will be the new goal clause:

¬ plus(X₂,Y₂,Z₂) (3.3)

which, in the current environment, equals

¬ plus(0,s(s(0)),Z₂) (3.4)

Suppose for the moment that our program also contains (some variant of) the clause

plus( 0, X₃, X₃ ) ¬ (3.5)

which is another true statement about the natural numbers and addition: the sum of zero and anything is that thing again. We can resolve the current goal with this clause with the mgu

{X₃=s(s(0)),Z₂=s(s(0))}.

Adding this to our constraint base, we get

{X₁=s(Z₂), X₂=0, Y₂=s(s(0)), X₃=s(s(0)),Z₂=s(s(0))},

which, in solved form, would be

{X₁=s(s(s(0))), X₂=0, Y₂=s(s(0)), X₃=s(s(0)), Z₂=s(s(0))}.

We have derived the empty clause, so our derivation succeeds. The answer to our original goal, in which X (renamed to X₁) was the only variable, will be reported as ``X=s(s(s(0))). According to our intended interpretation of this notation, this is the correct answer. We have proved that 1+2=3 . (Three cheers!)

Unification is an extremely versatile operation, and is used in Prolog to implement

the construction of new expressions from old,
the decomposition of one expression into several component expressions,
testing, branching and reasoning by cases,
parameter passing.

In the above example, unification was used to build up the value of the goal variable X: first we unified X with s(Z₂), then we unified Z₂ with s(s(0)). We also used unification to take apart the original first term of the addition: unifying s(0) with s(X₂) in effect stripped off the first (and only) s from s(0), leaving behind the solution for X₂. We also used unification for branching. Our first selected atom unified with the first program clause and not with the second (s(s(0)) does not unify with 0). The situation was reversed in the next step: our selected atom unified only with the head of the second clause (0 does not unify with s(X), for any X). Parameter passing by unification is pervasive in this and every example of SLD resolution; every time we unified a selected atom with the head of a program clause, we passed information from the goal down to the program clause by constraining the values of its parameter variables.

This document was translated from L^AT_EX by H^EV^EA.