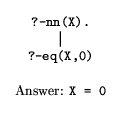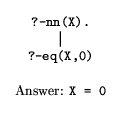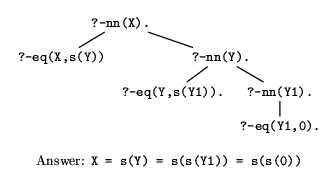Chapter 4 Anatomy of a Prolog Program

Now we have all of the pieces we need. Let's put together a Prolog program and see how it works. We will begin with an extremely simple, almost trivial program.

eq( X, X ).

Prolog Syntax Note: In Prolog we write fact clauses (more usually called unit clauses) without the arrow, and terminated by a period. So this piece of (Edinburgh) Prolog syntax corresponds to the (mathematical) clause ``eq(X,X)Ź ''.

On the face of it, this program is useless. It just tells us what everybody already knows: everything equals itself. But in fact it gives us a little more. Because of the way Prolog works, this predicate gives us direct access to Prolog's unification operation. Consider for example the following goal clause.

?- eq(sum(0,4,X1), sum(0,X2,X2)).

More Prolog Syntax: In these notes, goal clauses are written with a ?- symbol instead of the expected Ź . The ?- symbol is the Prolog interpreter's prompt. You don't type this! The interpreter will type it for you. Note that all clauses are terminated with a period.

Following the description of the Resolution Rule outlined in the last chapter, the first thing we need to do is to find a program clause whose head unifies with the goal. Our program has only one clause in it, so we don't have far to look! Now, the selected goal expression and the head of our selected program clause unify if and only if there is a substitution which makes them identical. So we are presented with the following unification problem:

eq(sum(0,4,X1), sum(0,X2,X2)) = eq( X, X ) .

Applying the term decomposition rule, we derive the new equations

X = sum(0,4,X1), X = sum(0,X2,X2) .

We can apply variable elimination using either equation; we will use the first. We add the new equation

sum(0,4,X1) = sum(0,X2,X2)

to the system. We can apply term decomposition again, yielding the following new equations.

0 = 0, X2 = 4, X1 = X2

The first is trivial and can be deleted from the system. Then we eliminate X2, to yield the following.

X1 = 4

Eliminating X1 yields a system in solved form. In particular,

X1 = 4, X2 = 4 .

There is another way to arrive at a solution to the unification problem. In this case, we think of the problem in the following terms.

eq(sum(0,4,X1), sum(0,X2,X2))q = eq( X, X )q

We are to solve for the unknown substitution q. Scanning these two expressions from left to right, we find that we first require the substitution

q₁ = {X / sum(0,4,X1) }.

Applying this substitution, we reduce our unification problem to the following simpler problem.

eq(sum(0,4,X1), sum(0,X2,X2))q = eq(sum(0,4,X1), sum(0,4,X1))q

We know in addition that q must satisfy the additional constraint that it include the substitution q₁ which we have just discovered. (Formally, we know that q must satisfy the equation q = q₁s for some yet-to-be-discovered s.)

Now, considering the second argument position, the roots of the two expressions are identical (they are both sum), and the first arguments of the sum-expressions also unify (they are both constants and identical). The first point at which our two expressions differ is where one contains X2 and the other contains 4. Since X2 is a variable, we know we need the variable binding X2/4. Applying the new substitution q₂ = {X2/4}, we reduce the unification problem to the following:

eq(sum(0,4,X1), sum(0,4,4))q = eq(sum(0,4,X1), sum(0,4,X1))q

where, in addition, q must satisfy q = q₁q₂s' , for some yet-to-be-discovered s'. (So you can see how we are building up our solution little by little as we learn more about the bindings of our unknowns.)

Finally, we discover the binding X1/4 and we are done. The solution to our orginal goal is found by composing all of the substitutions we have discovered along the way, and applying the resulting substitution to the variables that we originally entered (i.e., X1 and X2). That is,

q	=	q₁q₂q₃
	=	{X / sum(0,4,X1) }{X2/4}{X1/4}
	=	{X / sum(0,4,4), X2/4, X1/4 }

and so now the answer is explicit: X1 = 4, X2 = 4 .

Logically speaking we have in effect asked Prolog if there exist values for X1 and X2 which make true the formula

eq(sum(0,4,X1), sum(0,X2,X2)).

Prolog has discovered that our program has among its consequences that if X1 = 4 and X2 = 4 are true, then our original goal is true as well.

So we see that this program is not completely trivial. When we give it two inputs which are not in fact identical, but are unifiable, this one-clause program will actually unify them and produce as an answer their most general unifier:

X1	=	4
X2	=	4

This example is a little subtle, and you should be certain you understand it because it expresses a very important basic feature of Prolog: Equality means unifiability. In fact, the meaning of the 2-place predicate symbol `=' (or rather `=/2') which is built into Prolog is exactly the meaning we have given eq/2. That is, =/2 could have been (and in some Prologs it is) defined by the single fact-clause

X = X.

For the moment we will continue to use eq/2, but the reader should be prepared for us to switch back into standard Prolog without further comment.

Now we can extend this simple program a little. The following clauses implement a bit of Number Theory in Prolog. The intended interpretation of the predicate name nn/1 is ``natural number''.

eq(X,X).          

nn(X) :- eq(X,0). 
nn(X) :- eq(X,s(Y)), nn(Y).

More Prolog Syntax: This predicate introduces rule clauses. In rule clauses, the arrow is represented `:-'. Once again, rule clauses like all clauses are terminated with a period.

Suddenly, just by adding this single predicate to our program, we have a lot of new things to talk about.

We intend by these two clauses to provide a definition of the predicate nn/1. First, note that the definition is in two parts. In programming languages like Pascal or C when we define a procedure or function we provide a unique definition of that procedure or function. Languages like Pascal and C are deterministic. If we execute a call to a procedure p, we do not expect the program to have to decide which p we might mean. Prolog is non-deterministic. Logically speaking, we have no right to presume that the Prolog interpreter will select one or the other clause; good programming style demands that we be prepared for either choice. In fact, of course, since Prolog is implemented on a deterministic computing machine, its choice is entirely predictable: it will always try the first clause first.

So far so good, but what if the selected clause (i.e., the first clause) doesn't work? More concretely, suppose we type in the goal clause

nn(s(0)).

The goal unifies with the head of the first clause yielding the new goal clause

?- eq(s(0),0).

This goal cannot be solved by this program: the two expressions s(0) and 0 cannot be unified, so they cannot be made eq. Put another way, the goal is not a logical consequence of the program.

When this happens, Prolog backtracks. The Prolog interpreter keeps track of every point of the computation at which it had a choice to make. When the computation fails, as in this example, the Prolog interpreter checks its list of choice-points and returns to the most recent one, and proceeds by making a different choice of program clause. If it runs out of alternatives without finding one that works, then it must backtrack even further to a previous choice-point. Only when it runs out of alternatives and choice-points does it finally give up and report that the problem has no solution.

In the current example, the attempt to solve eq(s(0),0) will fail, so the interpreter will look for alternatives. There is only one way to solve eq/2 goals, so there are no alternatives to try there. The last choice-point was in solving the nn/1 goal. So the interpreter will backtrack to that point, so that the current goal once again is

?- nn(s(0)).

Now it will try solving that goal using the other clause in the definition of nn/1, so the new goal clause will be

?- eq(s(0),s(Y)), nn(Y).

This new goal clause introduces another feature of Prolog. The second clause defines nn/1 in terms of itself. This kind of definition is called recursive. On the surface it looks like we have introduced a piece of circular reasoning, the deductive equivalent of an infinite loop. But this is not in fact the case. To see that this is so, let us continue with the example, and see what happens. Once again, the new goal is

?- eq(s(0),s(Y)), nn(Y).

Prolog will select the leftmost sub-expression of the goal, namely

eq(s(0),s(Y)).

We can see that this has a simple solution which will require that Y be equal to 0.

Exercise: Work out this subproblem in detail and verify that this is indeed the solution.

The definition of eq/2 is a fact, that is, a clause with no body, so after solving eq(s(0),s(Y)), we simply remove it from the goal, and we derive the new goal

?- nn(0).

This has an immediate solution using the first clause of the definition. We have reduced our problem to facts; we have no more goals to solve, and so we have successfully established that nn(s(0)) is indeed a consequence of our program. Note that only the first clause will succeed for the goal ?- nn(0). The second clause will fail. (Why?) So in fact there is no infinite loop. The program halts and reports the correct answer. This example is summarised in Table 4.1.

1.

Current Goal: ?- nn(s(0)).

Selected Clause: nn(X1) :- eq(X1,0).

Solution Substitution: {X1/s(0)}

2.

Goal: ?- eq(s(0),0).

Clause: eq(X2,X2).

Solution: (Fails---no substitution can be found.)

2.

(Backtracking...)

Goal: ?- eq(s(0),0).

Clause: (Fails---no more clauses for eq/2.)

1.

(Backtracking...)

Goal: ?- nn(s(0)).

Clause: nn(X1) :- eq(X1,s(Y1)), nn(Y1).

Solution: {X1/s(0)}

2.

Goal: ?- eq(s(0),s(Y1)), nn(Y1).

Clause: eq(X2,X2).

Solution: {X2/s(0), Y1/0}

3.

Goal: ?- nn(0).

Clause: nn(X3) :- eq(X3,0).

Solution: {X3/0}

4.

Goal: ?- eq(0,0).

Clause: eq(X4,X4).

Solution: {X4/0}

5.

Goal: (The goal is empty; we're done!)

Table 4.1: Summary of the computation of the goal ?- nn(s(0)).

The reason that this apparently circular code actually halts is the key to the successful use of recursion in writing computer programs. In a certain sense that we can define rigorously, every time we called nn/1, the problem we wanted to solve got smaller. Ultimately, it got small enough so that we could solve it directly, using the (non-recursive) first clause.

Every example of a (well-written) recursive predicate that you will ever see has the same basic structure. The set of clauses defining a particular predicate must include some which are not recursive. These clauses form what is called the base of the recursion. In this example, and indeed in most examples, there is a single base-clause: the first clause in the definition of nn/1. The second clause in the definition of nn/1 is an example of what is called the recursive step, the processing step in which the procedure calls itself. In this case, the call to eq/2 which precedes the recursive call to nn/1 does two things. First, it assures that the value of X is in fact of the form s(Y), that is, X is the application of the s-function to some argument. Second it actually extracts that argument as the value of Y.¹ Then nn/1 calls itself again, but this time on Y instead of X. Every time we extract the argument of s in X we wind up with a strictly smaller expression---if X is finite (which we can safely assume that it is, since a user is presumed to have typed it in in less than a whole lifetime!), then clearly we can do this only a finite number of times before there is nothing else to extract.

Exercise: Neither (a) s(s(s(a))) nor (b) s(s(s(f(f(f(a)))))) is a natural number, according to our definition. Therefore, at some point processing must fail in each case. How many calls to nn/1 will be necessary before failure is detected?

We can think of the predicate nn/1 as defining a new data type. However, in many ways our logically-based definition of this data type is more useful than the sorts of definitions we find in other programming languages. We can use it either to recognize a particular data item as being of type natural number, (as in the example, where we essentially checked that s(0) was indeed of the type natural-number)---this is the standard task of data type definitions---or we can use it to generate new data items of the that type. Consider now the goal:

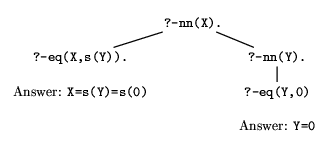
?- nn( X ).

We can think of this goal as expressing the question ``Which X's are natural numbers?'' Obviously, if we have written our definition correctly, there should be an infinite number of answers, so we will not consider all the possible proofs of this goal here, but here are a few, presented as proof trees, in figures 4.1--4.3. Proof trees should be read as follows: nodes are labeled with goals; if a node is labeled A and its daughters are labeled B₁, ..., B_n , then there must exist a program clause of which A :- B₁,...,B_n is an instance; that's the clause that was resolved against at this point in the proof.²

Figure 4.1: One way of answering ?- nn( X ).

Figure 4.2: Another way of answering ?- nn( X ).

Figure 4.3: Yet another way of answering ?- nn( X ).

Considering figures 4.1--4.3, one can easily see how an infinite number of proofs could be constructed, each yielding a different value for X.

Now let us extend our program yet again, introducing a new 2-place predicate symbol lt/2, which we intend to mean ``less than''.

lt(X,Y) :- 
    eq(X,0), 
    eq(Y,s(_)).
       
lt(X,Y) :- 
    eq(X,s(X0)), 
    eq(Y,s(Y0)),  
    lt(X0,Y0).

More Prolog Syntax: The underscore character appearing in the first clause of lt/2 is the anonymous variable. Every time it appears it causes Prolog to generate a new variable that it hasn't used yet. Note that f(X,X) implicitly constrains both arguments of f to be identical; this is not true of f(_,_), quite the contrary! The anonymous variable is used in this example because we are only interested in pattern-matching. We are not actually interested in the value of the argument of s; we only wish to ensure that it has one. Note that the meaning of this definition would not change if we replaced ``_'' with Z, say, but the code is more readable this way.

The definition of lt/2 presents us with no new problems or concepts. It is based on the fact that for any pair of natural numbers X and Y,

X < Y Ű 0 < (Y-X).

Zero is less than any natural number other than zero, and all natural numbers other than zero match the pattern s(_), that is, they are all successors of some other natural number. Zero is the only natural number which is not someone else's successor. The base clause expresses this fact. What remains is to prove that, given arbitrary inputs for X and Y, we will only reach the base of the recursion when the second argument has been reduced to Y minus X.

We actually prove this fact backwards. If a given goal is truly an instance of the less-than relation, that is, for given X and Y, if it truly is the case that X<Y, then it must be a fact that 0 < (Y-X). Now it is also a fact that

X < Y Ţ (X+1) < (Y+1),

for any pair of natural numbers X and Y. So if 0 < (Y-X), then 0+1 < (Y-X)+1 (which equals (Y+1)-X of course), and 0+1+1 < (Y+1+1)-X , and so forth. If we do this exactly X times, we will have established that 0+X < (Y+X)-X , that is, X < Y .

Though rather informal, this style of reasoning closely parallels mathematical proofs by induction. There is, in general, a strong connection between inductive proofs and recursive definitions (in fact, sometimes recursive definitions are called inductive definitions, especially in older works). This is why so many computer scientists favor recursion as a way of implementing repetetive computational procedures: the recursive style of definition makes available all the tremendously powerful tools that mathematicians have developed for doing proofs by induction.

Consider now the definition of lte/2, given below, and intended to mean ``less than or equal to.''

lte(X,Y) :- lt(X,Y).
lte(X,Y) :- eq(X,Y).

Since we already have definitions of ``less than'' and ``equal to'' all we need is some way of representing ``or''. We get this from the non-determinism of Prolog. Prolog is free to search for a solution using either clause, and as long as a solution exists using one of these clauses, Prolog will find it. A little more formally, a Prolog program is equivalent to a conjunction of implications like the following.

(lt(X,Y)Ţ lte(X,Y)) Ů (eq(X,Y) Ţ lte(X,Y))

This is provably equivalent to the formula

(lt(X,Y) Ú eq(X,Y)) Ţ lte(X,Y).

Exercise: Consider the following laws from propositional logic.

DeMorgan's Laws

Ź(p Ů q) ş (Ź p Ú Ź q)
Ź(p Ú q) ş (Ź p Ů Ź q)

Distributivity

p Ů (q Ú r) ş (p Ů q) Ú (p Ů r)
p Ú (q Ů r) ş (p Ú q) Ů (p Ú r)

Implication Defined
(p Ţ q) ş (Ź p Ú q)
Use them to show that
((q Ţ p) Ů (r Ţ p)) ş ((q Ú r) Ţ p).

Finally, consider the following definition of plus/3, a 3-place predicate defining addition.

plus(X,Y,Z) :- 
    eq(X,0), 
    eq(Y,Z).
plus(X,Y,Z) :- 
    eq(X,s(X0)), 
   eq(Z,s(Z0)), 
    plus(X0,Y,Z0).

This code implements the addition operation on natural numbers. Normally we think of addition as a two-place function, rather than a (three-place) predicate. In Prolog, ``functions'', that is, term-expressions other than constants and variables, are data structures, and ``real'' functions are computed via predicates. This situation is unusual enough to warrant treatment at some length.

4.1 A Note on Functions and Predicates

As we just noted, functions, that is, compound terms or non-trivial expression trees with function-symbols labeling their roots, are data structures. They are not evaluated. So for example the goals

?- p( 2+2 ).

and

?- p( 4 ).

are completely different goals. Prolog will not evaluate the expression 2+2 unless you tell it to, explicitly. That is, unless you provide Prolog with a theory of arithmetic which has among its consequences that 2+2 is (arithmetically) equal to 4, then all Prolog knows is that these are two distinct expression trees. The expression 2+2 is semantically identical to the expression 4 , at least if we interpret `+', `2' and `4' in the normal way, but it is syntactic identity that Prolog cares about.

In Prolog it is the predicates that actually get evaluated, so our intuitive notion of a function is usually implemented in Prolog as a predicate. There is no logical difficulty with this. Formally, we can always write

f(x₁,...,x_n) = x_n+1

as the predication

p(x₁,...,x_n,x_n+1)

as long as we then define it in such a way that it is true, given x₁,...,x_n , just in case (a) there is a unique x_n+1 making p true and (b) the value of that x_n+1 is exactly the value of f(x₁,...,x_n) . That is, p is defined so as to be true only in the case where

p(x₁,...,x_n,f(x₁,...,x_n)).

This is what we are doing with the predicate plus/3. We say ``let plus/3 be defined so that, for natural numbers X , Y , and Z , plus(X,Y,Z) is true whenever Z = X+Y .'' Here is the code for plus/3 again.

plus( X, Y, Z ) :-  
    X = 0, 
    Z = Y.
plus( X, Y, Z ) :- 
    X = s(X0), 
    Z = s(Z0), 
    plus( X0, Y, Z0 ).

Here, in the standard functional language of ordinary mathematics, are the conditions this code is meant to establish, more or less as they would appear in a text on number theory.

0 + Y = Y (4.1)

s(X0) + Y = s(X0+Y) (4.2)

It will now be our task to prove that the Prolog code corresponds to these specifications. This is an important goal in its own right: we must always be prepared to prove that our programs are correct implementations of their specifications. Here, however, we are more interested in the proof because it sheds a lot of light on how to translate back and forth between the language of functions and the language of predicates.

We begin with the first clause. We want to show that, if X = 0 , then X+Y = Y . We know from the intended interpretation of the predicate that X+Y = Z , that is, Z is intended as a name for the sum of X and Y . So X+Y=Y and X+Y=Z can only both hold if Y=Z , which is exactly the condition our program enforces. Put another way, we have shown that if we begin our computation in a state in which X = 0 , then, after executing a call to plus(X,Y,Z), we will wind up in a state in which Y=Z . Put yet another way, we are guaranteed that, for natural numbers X , Y , and Z , the following Prolog goal will always succeed.

?- X=0, plus(X,Y,Z), Z=Y.

It would be nice if we could just use Prolog in the same way to prove the correctness of the second clause. We would then like to be able to prove the goal:

?- X=s(X0), plus(X,Y,Z), Z=s(X0+Y).

Or, more compactly,

?- plus(s(X0),Y,s(X0+Y)).

This goal corresponds almost exactly to the condition in (4.2). But we know already that this goal will not succeed, because X0+Y is syntactically distinct from the representation of the number which is the sum of the numbers denoted by X0 and Y . It is, in fact, syntactically distinct from the representation of any natural number in our theory.

So here is the basic rule to follow. Wherever we mention an operation and we intend it to stand for its value, we must replace the operational expression (X0+Y in this example) with a variable, and call a predicate to compute the value of that variable from its arguments. In this example, we replace X0+Y with Z0, and call plus(X0,Y,Z0) to compute its value.

Note that we do not do this with expressions like s(X0) or s(Z0). This is because we do not intend to evaluate the successor function. It is part of our representation of natural numbers. (Or, to put it another way, ``natural numbers'' are just a subset of the expression trees, namely all and only those expression trees which are either of the form 0 or of the form s(X), where X is another member of the set of expression trees which we are calling ``natural numbers''.)

The same procedure applies in constructing the predicate exp/3, to implement exponentiation. The first clause

exp( X, Y, Z ) :- 
    Y = 0, 
    Z = s(0).

is straightforward, again. It transparently implements the arithmetical condition that X⁰ = 1 , and we could prove this directly in Prolog by issuing the goal

?- Y=0, exp(X,Y,Z), Z=s(0).

Or, more directly,

?- exp(X,0,s(0)).

But when Y = s(Y0) for some Y0, then things are complicated again. We would like to be able to establish that X^Y0⁺¹ = X*X^Y0 . But we cannot issue a goal like

?- exp( X, s(Y0), X*(X^ Y0) ).

Or rather, we can issue it, but it doesn't mean what we intend it to. Once again, this is because it includes expressions in places where what we really want is the semantic value of the expression. In particular, where we have written X*(X^ Y0) we do not mean the expression tree whose root is labeled `*' and whose subtrees are the expression trees X and X^ Y0. We actually mean the (successor-representation of) the natural number we get by multiplying X by the result of raising X to the Y0 power.

So, we apply our strategy again. We replace the arithmetic expression with a variable, Z, and we call the relevant predicate to compute the value of Z: times(X,X^ Y0,Z). But wait! This call to times/3 still contains an arithmetic expression---there is an expression tree where what we really want is (a data structure representing) the arithmetic value associated with the expression tree. So we must replace X^ Y0 with another variable, Z0, and call a Prolog predicate to compute the value of Z0: exp(X,Y0,Z0). Now we are done. We have ``unpacked'' all the arithmetic expressions, all of the ``function-calls'' in our original specification, and we get the clause:

exp( X, Y, Z ) :- 
    Y = s(Y0), 
    times( X, Z0, Z ), 
    exp( X, Y0, Z0 ).

1: This is an example of using unification in the first place for reasoning by cases---the first clause will only succeed if X is of the form 0; the second will only succeed if X is of the form s(Y) for some Y; all natural numbers are of one of these two forms, and no natural number is of both forms, so the call to eq/2 will cause the program to behave deterministically, even though in general Prolog clauses are non-deterministic. The same application of unification is also used to take the data structure which is the value of X and access one of its components, which becomes the value of Y. So we are doing both case-switching and data access all in one step---you may get some idea of the power and versatility of the unification operation!
2: Linguists: Note that we can think of program clauses (rule clauses, in particular) as grammar rules of the form AžŽ B₁... B_n , and proof trees as the derivation trees assigned to strings of fact clauses by this ``grammar''.

This document was translated from L^AT_EX by H^EV^EA.

Current Goal:	`?- nn(s(0)).`
Selected Clause:	`nn(X1) :- eq(X1,0).`
Solution Substitution:	{X1/s(0)}

Goal:	`?- eq(s(0),0).`
Clause:	`eq(X2,X2).`
Solution:	(Fails---no substitution can be found.)

(Backtracking...)
Goal:	`?- eq(s(0),0).`
Clause:	(Fails---no more clauses for eq/2.)

Goal:	`?- eq(s(0),s(Y1)), nn(Y1).`
Clause:	`eq(X2,X2).`
Solution:	{X2/s(0), Y1/0}